Question Number 171125 by mnjuly1970 last updated on 08/Jun/22
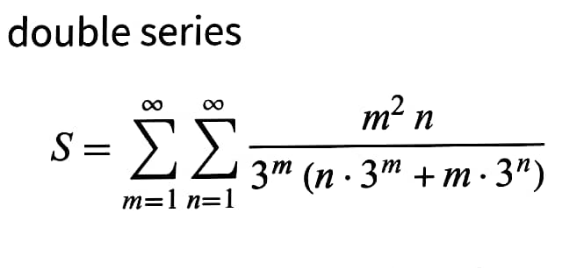
Answered by mindispower last updated on 09/Jun/22
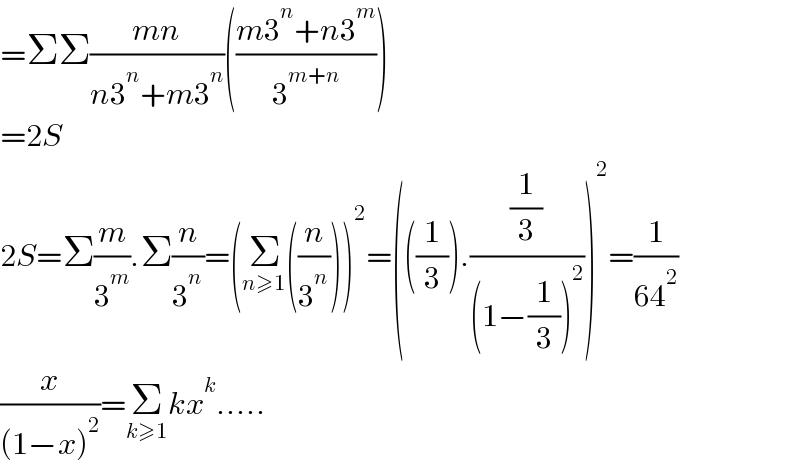
$$=\Sigma\Sigma\frac{{mn}}{{n}\mathrm{3}^{{n}} +{m}\mathrm{3}^{{n}} }\left(\frac{{m}\mathrm{3}^{{n}} +{n}\mathrm{3}^{{m}} }{\mathrm{3}^{{m}+{n}} }\right) \\ $$$$=\mathrm{2}{S} \\ $$$$\mathrm{2}{S}=\Sigma\frac{{m}}{\mathrm{3}^{{m}} }.\Sigma\frac{{n}}{\mathrm{3}^{{n}} }=\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{{n}}{\mathrm{3}^{{n}} }\right)\right)^{\mathrm{2}} =\left(\left(\frac{\mathrm{1}}{\mathrm{3}}\right).\frac{\frac{\mathrm{1}}{\mathrm{3}}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{64}^{\mathrm{2}} } \\ $$$$\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\underset{{k}\geqslant\mathrm{1}} {\sum}{kx}^{{k}} ….. \\ $$
Commented by mnjuly1970 last updated on 09/Jun/22
$${thanks}\:{alot}\:{sir}\:{power}\:… \\ $$
