Question Number 171179 by Mastermind last updated on 09/Jun/22

Answered by aleks041103 last updated on 09/Jun/22
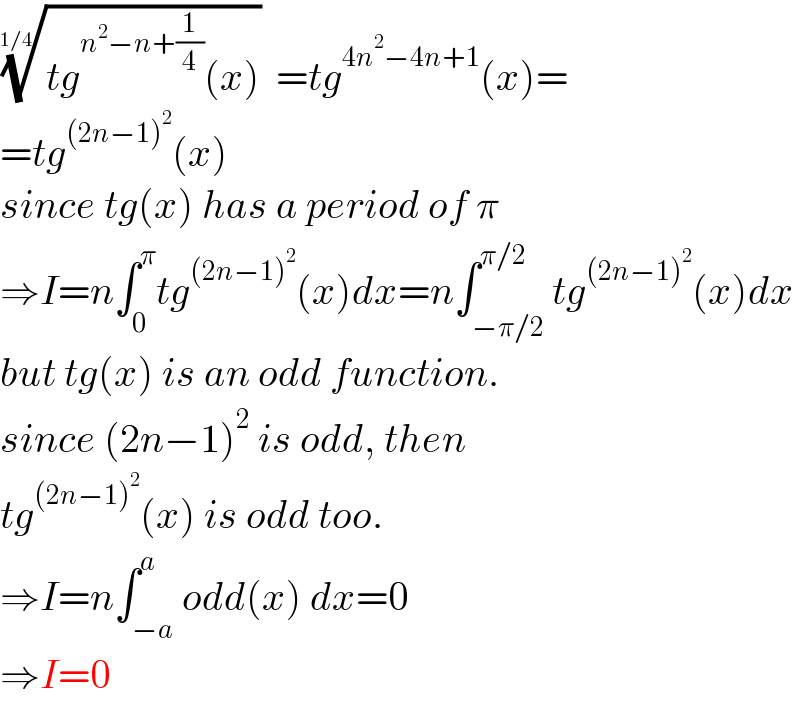
$$\sqrt[{\mathrm{1}/\mathrm{4}}]{{tg}^{{n}^{\mathrm{2}} −{n}+\frac{\mathrm{1}}{\mathrm{4}}} \left({x}\right)}={tg}^{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{4}{n}+\mathrm{1}} \left({x}\right)= \\ $$$$={tg}^{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \left({x}\right) \\ $$$${since}\:{tg}\left({x}\right)\:{has}\:{a}\:{period}\:{of}\:\pi \\ $$$$\Rightarrow{I}={n}\int_{\mathrm{0}} ^{\pi} {tg}^{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \left({x}\right){dx}={n}\int_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} {tg}^{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \left({x}\right){dx} \\ $$$${but}\:{tg}\left({x}\right)\:{is}\:{an}\:{odd}\:{function}. \\ $$$${since}\:\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} \:{is}\:{odd},\:{then} \\ $$$${tg}^{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} } \left({x}\right)\:{is}\:{odd}\:{too}. \\ $$$$\Rightarrow{I}={n}\int_{−{a}} ^{{a}} {odd}\left({x}\right)\:{dx}=\mathrm{0} \\ $$$$\Rightarrow{I}=\mathrm{0} \\ $$
Commented by Mastermind last updated on 09/Jun/22

$${Thanks} \\ $$
Commented by Mastermind last updated on 09/Jun/22
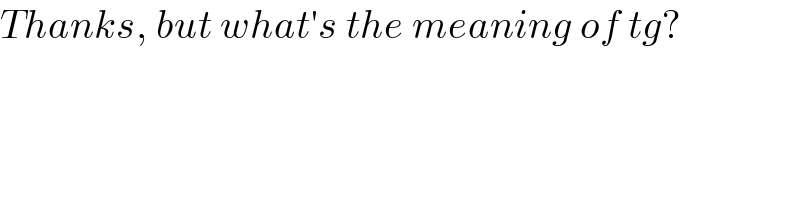
$${Thanks},\:{but}\:{what}'{s}\:{the}\:{meaning}\:{of}\:{tg}? \\ $$
Commented by aleks041103 last updated on 09/Jun/22

$${tg}\equiv{tan} \\ $$
