Question-171443

Question Number 171443 by cortano1 last updated on 15/Jun/22

Answered by Rasheed.Sindhi last updated on 15/Jun/22

{ ((((y+z)/x)=(1/(2x−1)))),((((x+z)/y)=(1/(3y−1)))),((((x+z)/z)=(1/(5z−1)))) :} { ((((y+z)/x)+1=(1/(2x−1))+1)),((((x+z)/y)+1=(1/(3y−1))+1)),((((x+z)/z)+1=(1/(5z−1))+1)) :} { ((((x+y+z)/x)=((2x)/(2x−1)))),((((x+y+z)/y)=((3y)/(3y−1)))),((((x+y+z)/z)=((5z)/(5z−1)))) :} { ((x+y+z=((2x^2 )/(2x−1)))),((x+y+z=((3y^2 )/(3y−1)) )),((x+y+z=((5z^2 )/(5z−1)))) :} ((2x^2 )/(2x−1))=((3y^2 )/(3y−1))=((5z^2 )/(5z−1)) ((2x−1)/(2x^2 ))=((3y−1)/(3y^2 ))=((5z−1)/(5z^2 ))=k(say) { ((2kx^2 −2x+1=0)),((3ky^2 −3y+1=0)),((5kz^2 −5z+1=0)) :} { ((x=((2±(√(4−8k)))/(4k)))),((y=((3±(√(9−12k)))/(6k)))),((z=((5±(√(25−20k)))/(10k)))) :} { ((x=((1±(√(1−2k)))/(2k)) → 1−2k>0⇒k<(1/2))),((y=((3±(√(9−12k)))/(6k))→ 9−12k>0⇒k<(3/4))),((z=((5±(√(25−20k)))/(10k))→25−20k>0⇒k<(5/4))) :} ⇒k<(1/2) If we search rational x,y,z then k=−60 provides those.

$$\begin{cases}{\frac{{y}+{z}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}}\\{\frac{{x}+{z}}{{y}}=\frac{\mathrm{1}}{\mathrm{3}{y}−\mathrm{1}}}\\{\frac{{x}+{z}}{{z}}=\frac{\mathrm{1}}{\mathrm{5}{z}−\mathrm{1}}}\end{cases}\:\:\:\: \\ $$$$\begin{cases}{\frac{{y}+{z}}{{x}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}+\mathrm{1}}\\{\frac{{x}+{z}}{{y}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{3}{y}−\mathrm{1}}+\mathrm{1}}\\{\frac{{x}+{z}}{{z}}+\mathrm{1}=\frac{\mathrm{1}}{\mathrm{5}{z}−\mathrm{1}}+\mathrm{1}}\end{cases}\:\:\:\: \\ $$$$\begin{cases}{\frac{{x}+{y}+{z}}{{x}}=\frac{\mathrm{2}{x}}{\mathrm{2}{x}−\mathrm{1}}}\\{\frac{{x}+{y}+{z}}{{y}}=\frac{\mathrm{3}{y}}{\mathrm{3}{y}−\mathrm{1}}}\\{\frac{{x}+{y}+{z}}{{z}}=\frac{\mathrm{5}{z}}{\mathrm{5}{z}−\mathrm{1}}}\end{cases}\:\:\:\: \\ $$$$\begin{cases}{{x}+{y}+{z}=\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}−\mathrm{1}}}\\{{x}+{y}+{z}=\frac{\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{3}{y}−\mathrm{1}}\:\:\:\:\:\:\:\:}\\{{x}+{y}+{z}=\frac{\mathrm{5}{z}^{\mathrm{2}} }{\mathrm{5}{z}−\mathrm{1}}}\end{cases}\:\:\:\: \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{2}{x}−\mathrm{1}}=\frac{\mathrm{3}{y}^{\mathrm{2}} }{\mathrm{3}{y}−\mathrm{1}}=\frac{\mathrm{5}{z}^{\mathrm{2}} }{\mathrm{5}{z}−\mathrm{1}} \\ $$$$\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }=\frac{\mathrm{3}{y}−\mathrm{1}}{\mathrm{3}{y}^{\mathrm{2}} }=\frac{\mathrm{5}{z}−\mathrm{1}}{\mathrm{5}{z}^{\mathrm{2}} }={k}\left({say}\right) \\ $$$$\begin{cases}{\mathrm{2}{kx}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}=\mathrm{0}}\\{\mathrm{3}{ky}^{\mathrm{2}} −\mathrm{3}{y}+\mathrm{1}=\mathrm{0}}\\{\mathrm{5}{kz}^{\mathrm{2}} −\mathrm{5}{z}+\mathrm{1}=\mathrm{0}}\end{cases}\:\:\: \\ $$$$\begin{cases}{{x}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{8}{k}}}{\mathrm{4}{k}}}\\{{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{12}{k}}}{\mathrm{6}{k}}}\\{{z}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{20}{k}}}{\mathrm{10}{k}}}\end{cases}\: \\ $$$$\begin{cases}{{x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{2}{k}}}{\mathrm{2}{k}}\:\rightarrow\:\mathrm{1}−\mathrm{2}{k}>\mathrm{0}\Rightarrow{k}<\frac{\mathrm{1}}{\mathrm{2}}}\\{{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{9}−\mathrm{12}{k}}}{\mathrm{6}{k}}\rightarrow\:\mathrm{9}−\mathrm{12}{k}>\mathrm{0}\Rightarrow{k}<\frac{\mathrm{3}}{\mathrm{4}}}\\{{z}=\frac{\mathrm{5}\pm\sqrt{\mathrm{25}−\mathrm{20}{k}}}{\mathrm{10}{k}}\rightarrow\mathrm{25}−\mathrm{20}{k}>\mathrm{0}\Rightarrow{k}<\frac{\mathrm{5}}{\mathrm{4}}}\end{cases}\: \\ $$$$\Rightarrow{k}<\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{search}\:\mathrm{rational}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{then} \\ $$$$\:\mathrm{k}=−\mathrm{60}\:\mathrm{provides}\:\mathrm{those}. \\ $$

Answered by MJS_new last updated on 15/Jun/22

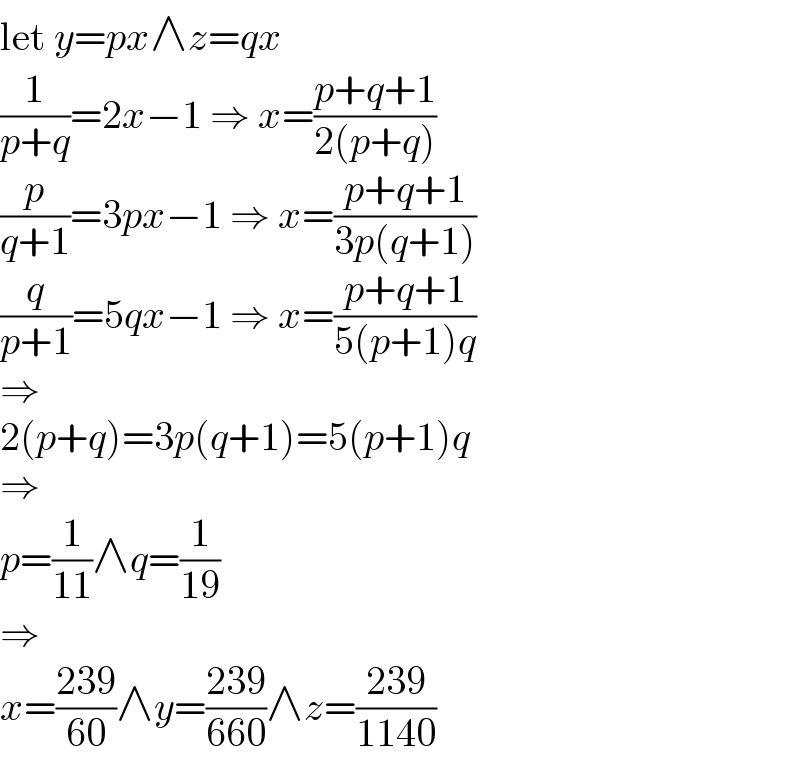
let y=px∧z=qx (1/(p+q))=2x−1 ⇒ x=((p+q+1)/(2(p+q))) (p/(q+1))=3px−1 ⇒ x=((p+q+1)/(3p(q+1))) (q/(p+1))=5qx−1 ⇒ x=((p+q+1)/(5(p+1)q)) ⇒ 2(p+q)=3p(q+1)=5(p+1)q ⇒ p=(1/(11))∧q=(1/(19)) ⇒ x=((239)/(60))∧y=((239)/(660))∧z=((239)/(1140))

$$\mathrm{let}\:{y}={px}\wedge{z}={qx} \\ $$$$\frac{\mathrm{1}}{{p}+{q}}=\mathrm{2}{x}−\mathrm{1}\:\Rightarrow\:{x}=\frac{{p}+{q}+\mathrm{1}}{\mathrm{2}\left({p}+{q}\right)} \\ $$$$\frac{{p}}{{q}+\mathrm{1}}=\mathrm{3}{px}−\mathrm{1}\:\Rightarrow\:{x}=\frac{{p}+{q}+\mathrm{1}}{\mathrm{3}{p}\left({q}+\mathrm{1}\right)} \\ $$$$\frac{{q}}{{p}+\mathrm{1}}=\mathrm{5}{qx}−\mathrm{1}\:\Rightarrow\:{x}=\frac{{p}+{q}+\mathrm{1}}{\mathrm{5}\left({p}+\mathrm{1}\right){q}} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}\left({p}+{q}\right)=\mathrm{3}{p}\left({q}+\mathrm{1}\right)=\mathrm{5}\left({p}+\mathrm{1}\right){q} \\ $$$$\Rightarrow \\ $$$${p}=\frac{\mathrm{1}}{\mathrm{11}}\wedge{q}=\frac{\mathrm{1}}{\mathrm{19}} \\ $$$$\Rightarrow \\ $$$${x}=\frac{\mathrm{239}}{\mathrm{60}}\wedge{y}=\frac{\mathrm{239}}{\mathrm{660}}\wedge{z}=\frac{\mathrm{239}}{\mathrm{1140}} \\ $$

Commented by infinityaction last updated on 15/Jun/22