Question Number 171456 by mathlove last updated on 15/Jun/22
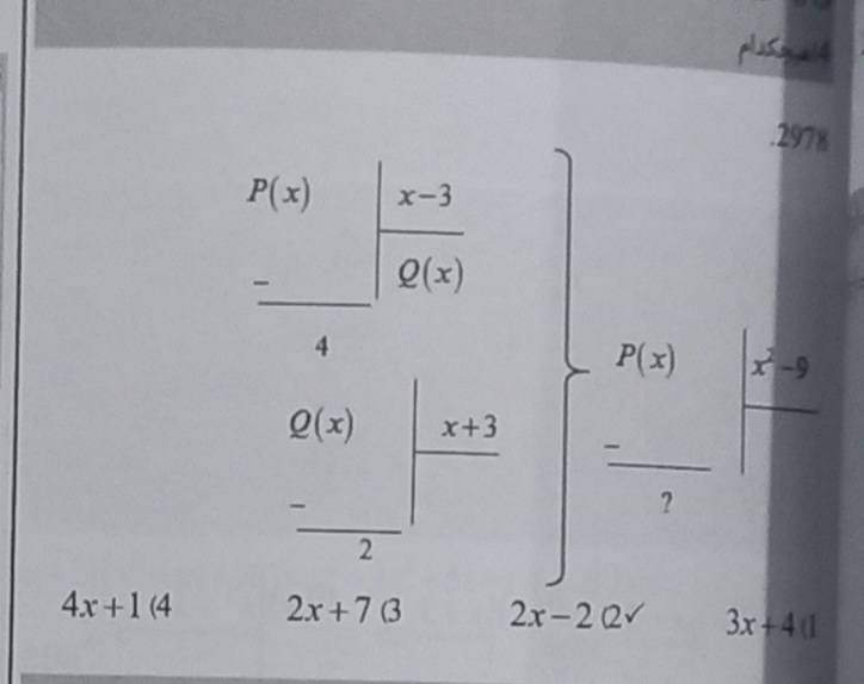
Commented by mathlove last updated on 16/Jun/22

$${solution}?? \\ $$
Answered by Rasheed.Sindhi last updated on 16/Jun/22

$${Let}\:{P}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$$\bullet\:{P}\left({x}\right)\:{is}\:{divided}\:{by}\:{x}−\mathrm{3}\:{leaving} \\ $$$$\:\:\:{remainder}\:\mathrm{4}.\:{By}\:{synthetic}\:{division}: \\ $$$$\begin{array}{|c|c|c|}{\left.\mathrm{3}\right)}&\hline{{a}}&\hline{{b}}&\hline{{c}}\\{}&\hline{}&\hline{\mathrm{3}{a}}&\hline{\mathrm{9}{a}+\mathrm{3}{b}}\\{}&\hline{{a}}&\hline{\mathrm{3}{a}+{b}}&\hline{\mathrm{9}{a}+\mathrm{3}{b}+{c}=\mathrm{4}^{\bigstar} }\\\hline\end{array} \\ $$$$\:\:{Q}\left({x}\right)={ax}+\left(\mathrm{3}{a}+{b}\right) \\ $$$$\bullet{Q}\left({x}\right)\:{is}\:{divided}\:{by}\:{x}+\mathrm{3}\:{leaving} \\ $$$$\:\:\:{remainder}\left({R}\right)\:\mathrm{2}. \\ $$$$\:\:\:{R}={Q}\left(−\mathrm{3}\right)={a}\left(−\mathrm{3}\right)+\left(\mathrm{3}{a}+{b}\right)=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{b}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:^{\bigstar} \:\mathrm{9}{a}+\mathrm{3}\left(\mathrm{2}\right)+{c}=\mathrm{4}\Rightarrow\mathrm{9}{a}+{c}=−\mathrm{2} \\ $$$$\bullet{P}\left({x}\right)\:{is}\:{divided}\:{by}\:{x}^{\mathrm{2}} −\mathrm{9} \\ $$$$\left.\:{x}^{\mathrm{2}} −\mathrm{9}\right)\overset{{a}} {{ax}^{\mathrm{2}} +{bx}+{c}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:_{−} {ax}^{\mathrm{2}} \:\:\:\:\:\:\:\:\underset{+} {−}\mathrm{9}{a} \\ $$$$\:{Remainder}:\:{bx}+\mathrm{9}{a}+{c}=\left(\mathrm{2}\right){x}+\left(−\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{x}−\mathrm{2}\:\:\:\:{ans} \\ $$
Commented by mathlove last updated on 16/Jun/22

$${thanks} \\ $$
