Question Number 171493 by Mastermind last updated on 16/Jun/22

Answered by mr W last updated on 16/Jun/22
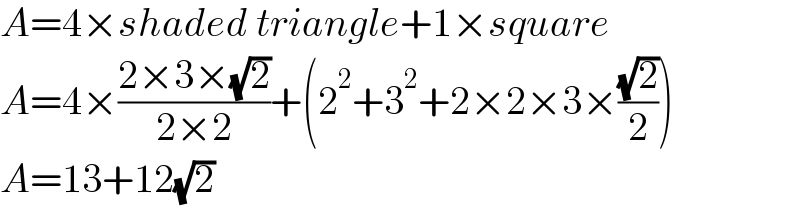
$${A}=\mathrm{4}×{shaded}\:{triangle}+\mathrm{1}×{square} \\ $$$${A}=\mathrm{4}×\frac{\mathrm{2}×\mathrm{3}×\sqrt{\mathrm{2}}}{\mathrm{2}×\mathrm{2}}+\left(\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} +\mathrm{2}×\mathrm{2}×\mathrm{3}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$${A}=\mathrm{13}+\mathrm{12}\sqrt{\mathrm{2}} \\ $$
Commented by mr W last updated on 16/Jun/22
Commented by Mastermind last updated on 16/Jun/22
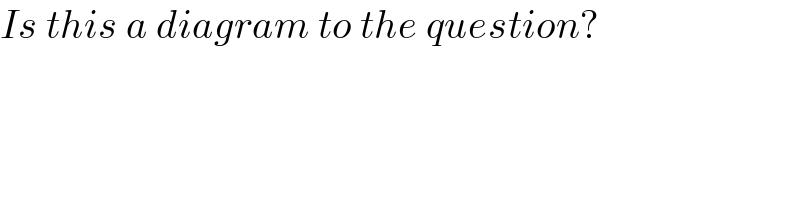
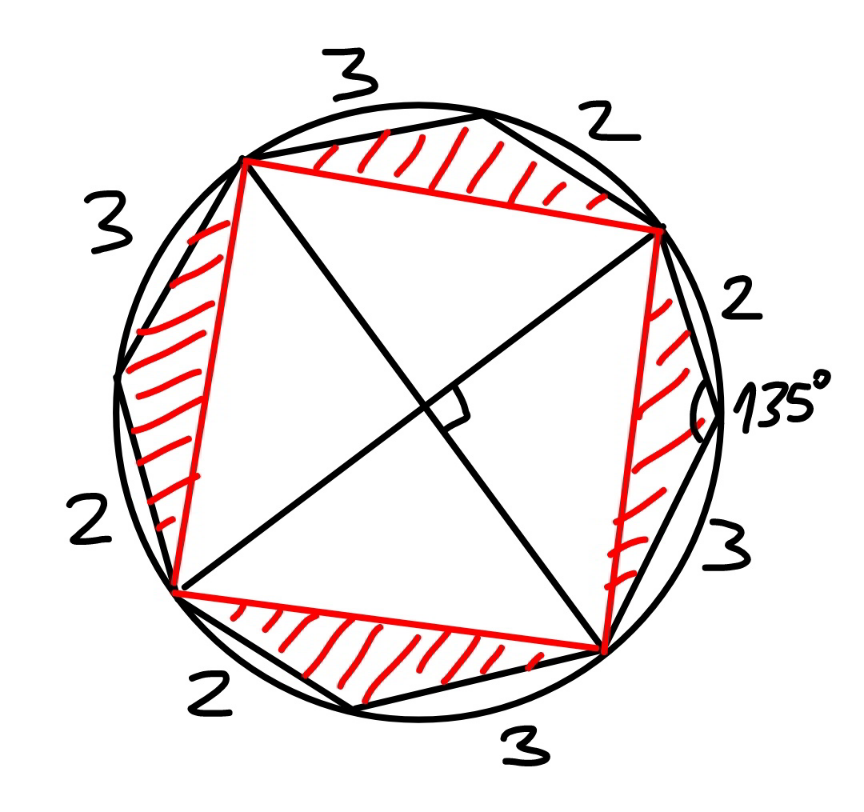
$${Is}\:{this}\:{a}\:{diagram}\:{to}\:{the}\:{question}? \\ $$
Commented by mr W last updated on 16/Jun/22

$${yes}. \\ $$$${why}\:{should}\:{i}\:{do}\:{it}\:{if}\:{it}\:{has}\:{nothing}\:{to} \\ $$$${do}\:{with}\:{the}\:{question}. \\ $$
Commented by mr W last updated on 17/Jun/22

$${let}'{s}\:{look}\:{at}\:{a}\:{n}−{side}−{polygon} \\ $$$${inscribed}\:{in}\:{a}\:{circle}.\:{the}\:{sides}\: \\ $$$${lengthes}\:{are}\:{a}_{\mathrm{1}} ,{a}_{\mathrm{2}} ,…{a}_{{i}} ,…{a}_{{n}} .\:{say}\:{the} \\ $$$${radius}\:{is}\:{R}.\:\:{we}\:{see}\:{that}\:{the}\:{area}\:{of}\:{the} \\ $$$${polygon}\:{is}\:{the}\:{sum}\:{of}\:{all}\:{n}\:{triangles} \\ $$$${with}\:{sides}\:{R},{a}_{{i}} ,{R}.\:{only}\:{the}\:{sum}\:{of} \\ $$$${the}\:{n}\:{triangles}\:{is}\:{important},\:{the}\:{order} \\ $$$${of}\:{the}\:{n}\:{triangles}\:{doesn}'{t}\:{matter}. \\ $$$${i}.{e}.\:{we}\:{can}\:{rearrange}\:{the}\:{n}\:{sides}\: \\ $$$${arbitrarily}\:{without}\:{changing}\:{the}\:{area} \\ $$$${of}\:{the}\:{inscribed}\:{polygon}. \\ $$
Commented by mr W last updated on 16/Jun/22

$${usually}\:{i}\:{don}'{t}\:{show}\:{every}\:{step}\:{when} \\ $$$${i}\:{try}\:{to}\:{solve}\:{a}\:{problem}.\:{certainly}\:{i} \\ $$$${know}\:{that}\:{the}\:{question}\:{says}\:“{four}\: \\ $$$${consecutive}\:{sides}\:{of}\:{length}\:\mathrm{3}\:{and}\:{four} \\ $$$${consecutive}\:{sides}\:{of}\:{length}\:\mathrm{2}''.\:{but}\:{for} \\ $$$${a}\:{polygon}\:{inscribed}\:{in}\:{a}\:{circle},\:{its} \\ $$$${area}\:{is}\:{independent}\:{in}\:{which}\:{order} \\ $$$${its}\:{sides}\:{are}\:{arranged}.\:{therefore}\:{i} \\ $$$${rearranged}\:{the}\:{order}\:{of}\:{the}\:{sides}\:{so} \\ $$$${that}\:{its}\:{area}\:{can}\:{be}\:{easily}\:{calculated}. \\ $$
Commented by mr W last updated on 16/Jun/22

Commented by Mastermind last updated on 17/Jun/22

$${Okay} \\ $$$${thanks}\:{big}\:{boss} \\ $$
Commented by Tawa11 last updated on 17/Jun/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
