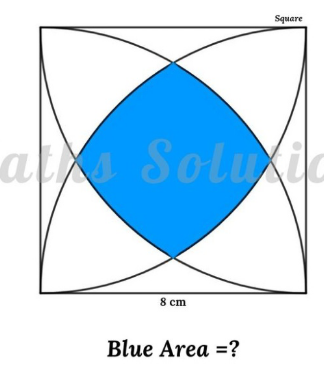
Question Number 171512 by infinityaction last updated on 16/Jun/22
Answered by som(math1967) last updated on 17/Jun/22
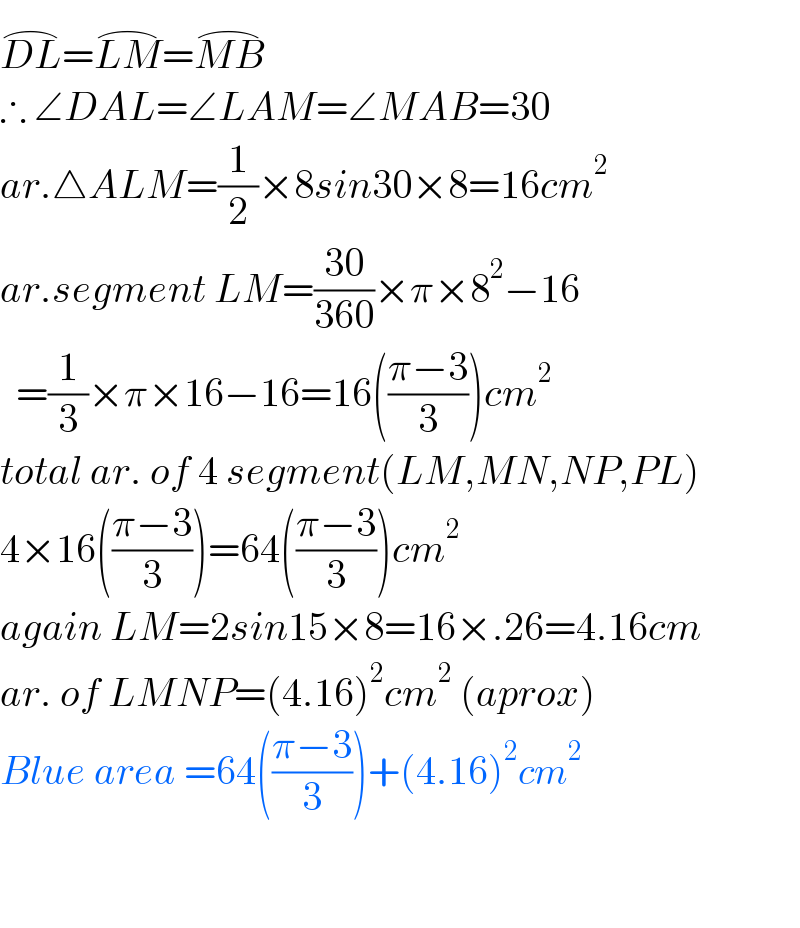
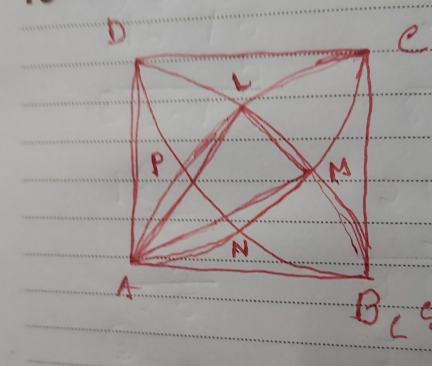
$$\overset{\frown} {{DL}}=\overset{\frown} {{LM}}=\overset{\frown} {{MB}} \\ $$$$\therefore\:\angle{DAL}=\angle{LAM}=\angle{MAB}=\mathrm{30} \\ $$$${ar}.\bigtriangleup{ALM}=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{8}{sin}\mathrm{30}×\mathrm{8}=\mathrm{16}{cm}^{\mathrm{2}} \\ $$$${ar}.{segment}\:{LM}=\frac{\mathrm{30}}{\mathrm{360}}×\pi×\mathrm{8}^{\mathrm{2}} −\mathrm{16} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}×\pi×\mathrm{16}−\mathrm{16}=\mathrm{16}\left(\frac{\pi−\mathrm{3}}{\mathrm{3}}\right){cm}^{\mathrm{2}} \\ $$$${total}\:{ar}.\:{of}\:\mathrm{4}\:{segment}\left({LM},{MN},{NP},{PL}\right) \\ $$$$\mathrm{4}×\mathrm{16}\left(\frac{\pi−\mathrm{3}}{\mathrm{3}}\right)=\mathrm{64}\left(\frac{\pi−\mathrm{3}}{\mathrm{3}}\right){cm}^{\mathrm{2}} \\ $$$${again}\:{LM}=\mathrm{2}{sin}\mathrm{15}×\mathrm{8}=\mathrm{16}×.\mathrm{26}=\mathrm{4}.\mathrm{16}{cm} \\ $$$${ar}.\:{of}\:{LMNP}=\left(\mathrm{4}.\mathrm{16}\right)^{\mathrm{2}} {cm}^{\mathrm{2}} \:\left({aprox}\right) \\ $$$${Blue}\:{area}\:=\mathrm{64}\left(\frac{\pi−\mathrm{3}}{\mathrm{3}}\right)+\left(\mathrm{4}.\mathrm{16}\right)^{\mathrm{2}} {cm}^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 17/Jun/22

$${thanks} \\ $$
Commented by som(math1967) last updated on 17/Jun/22
Commented by Tawa11 last updated on 17/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
