Question Number 171528 by cortano1 last updated on 17/Jun/22
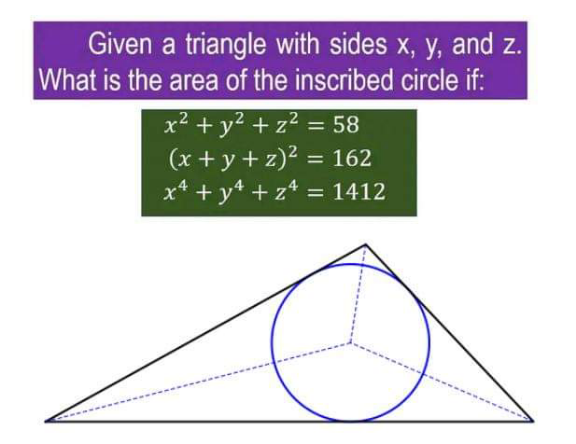
Answered by som(math1967) last updated on 17/Jun/22
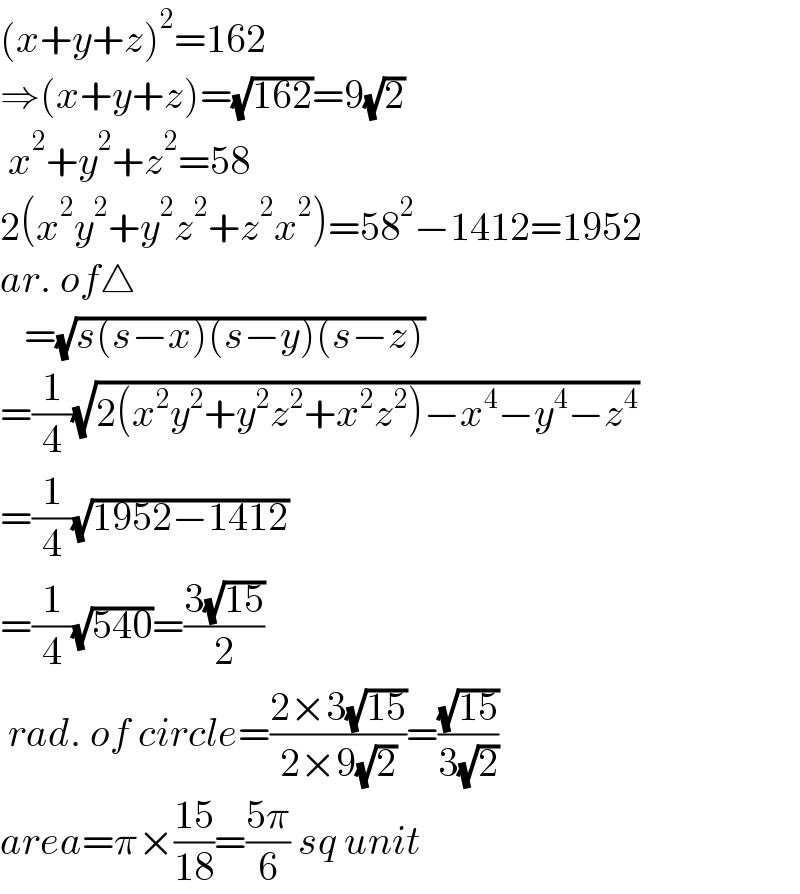
$$\left({x}+{y}+{z}\right)^{\mathrm{2}} =\mathrm{162} \\ $$$$\Rightarrow\left({x}+{y}+{z}\right)=\sqrt{\mathrm{162}}=\mathrm{9}\sqrt{\mathrm{2}} \\ $$$$\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{58} \\ $$$$\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right)=\mathrm{58}^{\mathrm{2}} −\mathrm{1412}=\mathrm{1952} \\ $$$${ar}.\:{of}\bigtriangleup \\ $$$$\:\:\:=\sqrt{{s}\left({s}−{x}\right)\left({s}−{y}\right)\left({s}−{z}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{x}^{\mathrm{2}} {z}^{\mathrm{2}} \right)−{x}^{\mathrm{4}} −{y}^{\mathrm{4}} −{z}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{1952}−\mathrm{1412}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{540}}=\frac{\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{2}} \\ $$$$\:{rad}.\:{of}\:{circle}=\frac{\mathrm{2}×\mathrm{3}\sqrt{\mathrm{15}}}{\mathrm{2}×\mathrm{9}\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{15}}}{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$${area}=\pi×\frac{\mathrm{15}}{\mathrm{18}}=\frac{\mathrm{5}\pi}{\mathrm{6}}\:{sq}\:{unit} \\ $$
Commented by Tawa11 last updated on 17/Jun/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
