Question-171529

Question Number 171529 by cortano1 last updated on 17/Jun/22

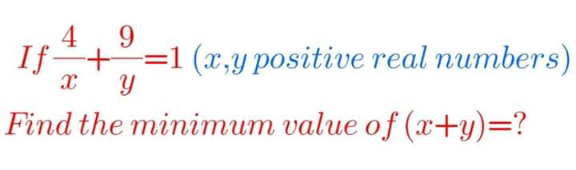
Commented by kapoorshah last updated on 17/Jun/22

$$\mathrm{25} \\ $$

Answered by FelipeLz last updated on 17/Jun/22

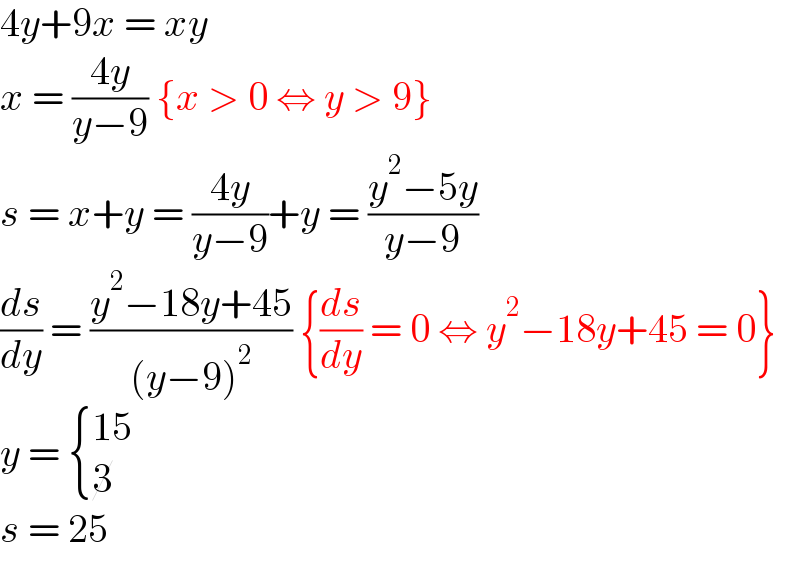
4y+9x = xy x = ((4y)/(y−9)) {x > 0 ⇔ y > 9} s = x+y = ((4y)/(y−9))+y = ((y^2 −5y)/(y−9)) (ds/dy) = ((y^2 −18y+45)/((y−9)^2 )) {(ds/dy) = 0 ⇔ y^2 −18y+45 = 0} y = { ((15)),(3) :} s = 25

$$\mathrm{4}{y}+\mathrm{9}{x}\:=\:{xy} \\ $$$${x}\:=\:\frac{\mathrm{4}{y}}{{y}−\mathrm{9}}\:\left\{{x}\:>\:\mathrm{0}\:\Leftrightarrow\:{y}\:>\:\mathrm{9}\right\} \\ $$$${s}\:=\:{x}+{y}\:=\:\frac{\mathrm{4}{y}}{{y}−\mathrm{9}}+{y}\:=\:\frac{{y}^{\mathrm{2}} −\mathrm{5}{y}}{{y}−\mathrm{9}} \\ $$$$\frac{{ds}}{{dy}}\:=\:\frac{{y}^{\mathrm{2}} −\mathrm{18}{y}+\mathrm{45}}{\left({y}−\mathrm{9}\right)^{\mathrm{2}} }\:\left\{\frac{{ds}}{{dy}}\:=\:\mathrm{0}\:\Leftrightarrow\:{y}^{\mathrm{2}} −\mathrm{18}{y}+\mathrm{45}\:=\:\mathrm{0}\right\} \\ $$$${y}\:=\:\begin{cases}{\mathrm{15}}\\{\cancel{\mathrm{3}}}\end{cases} \\ $$$${s}\:=\:\mathrm{25} \\ $$

Commented by kapoorshah last updated on 17/Jun/22

$${nice} \\ $$

Answered by som(math1967) last updated on 17/Jun/22

(4/x)+(9/y)=1 y=((9x)/(x−4)) x+y =x+((9x)/(x−4))=f(x) let f^l (x)=1+((9(x−4)−9x)/((x−4)^2 ))=1−((36)/((x−4)^2 )) f^(ll) (x)= ((72)/((x−4)^3 )) for max or min f^l (x)=0 ∴ 1−((36)/((x−4)^2 ))=0 ⇒(x−4)=±6∴ x=10 or−2 f^(ll) (10)=((72)/6^3 )>0 ∴ min (x+y)=10+((90)/6)=25

$$\:\frac{\mathrm{4}}{{x}}+\frac{\mathrm{9}}{{y}}=\mathrm{1} \\ $$$$\:{y}=\frac{\mathrm{9}{x}}{{x}−\mathrm{4}} \\ $$$$\:{x}+{y} \\ $$$$={x}+\frac{\mathrm{9}{x}}{{x}−\mathrm{4}}={f}\left({x}\right)\:\:{let} \\ $$$${f}^{{l}} \left({x}\right)=\mathrm{1}+\frac{\mathrm{9}\left({x}−\mathrm{4}\right)−\mathrm{9}{x}}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{36}}{\left({x}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${f}^{\boldsymbol{{ll}}} \left(\boldsymbol{{x}}\right)=\:\frac{\mathrm{72}}{\left(\boldsymbol{{x}}−\mathrm{4}\right)^{\mathrm{3}} } \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{max}}\:\boldsymbol{{or}}\:\boldsymbol{{min}}\:\boldsymbol{{f}}^{\boldsymbol{{l}}} \left(\boldsymbol{{x}}\right)=\mathrm{0} \\ $$$$\therefore\:\mathrm{1}−\frac{\mathrm{36}}{\left(\boldsymbol{{x}}−\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{4}\right)=\pm\mathrm{6}\therefore\:{x}=\mathrm{10}\:{or}−\mathrm{2} \\ $$$$\boldsymbol{{f}}^{\boldsymbol{{ll}}} \left(\mathrm{10}\right)=\frac{\mathrm{72}}{\mathrm{6}^{\mathrm{3}} }>\mathrm{0} \\ $$$$\therefore\:{min}\:\left({x}+{y}\right)=\mathrm{10}+\frac{\mathrm{90}}{\mathrm{6}}=\mathrm{25} \\ $$$$ \\ $$

Commented by kapoorshah last updated on 17/Jun/22

$${nice} \\ $$

Answered by greougoury555 last updated on 18/Jun/22

(4/x)+(9/y) = 1 (2^2 /x) +(3^2 /y) = 1 1 ≥ (((2+3)^2 )/(x+y)) ⇒x+y ≥ 25 (min) when (2/x) = (3/y) = (1/5)

$$\:\frac{\mathrm{4}}{{x}}+\frac{\mathrm{9}}{{y}}\:=\:\mathrm{1} \\ $$$$\:\frac{\mathrm{2}^{\mathrm{2}} }{{x}}\:+\frac{\mathrm{3}^{\mathrm{2}} }{{y}}\:=\:\mathrm{1} \\ $$$$\:\mathrm{1}\:\geqslant\:\frac{\left(\mathrm{2}+\mathrm{3}\right)^{\mathrm{2}} }{{x}+{y}}\: \\ $$$$\:\Rightarrow{x}+{y}\:\geqslant\:\mathrm{25}\:\left({min}\right) \\ $$$$\:{when}\:\frac{\mathrm{2}}{{x}}\:=\:\frac{\mathrm{3}}{{y}}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$

Answered by floor(10²Eta[1]) last updated on 17/Jun/22

4y+9x=xy AM≥GM: ((4y+9x)/2)≥(√((4y)(9x))) ((xy)/2)≥(√(36xy)) xy≥12(√(xy)) (xy)^2 ≥144xy xy(xy−144)≥0⇒xy≥144 ((x+y)/2)≥(√(xy))≥(√(144))=12 x+y≥24

$$\mathrm{4y}+\mathrm{9x}=\mathrm{xy} \\ $$$$\mathrm{AM}\geqslant\mathrm{GM}: \\ $$$$\frac{\mathrm{4y}+\mathrm{9x}}{\mathrm{2}}\geqslant\sqrt{\left(\mathrm{4y}\right)\left(\mathrm{9x}\right)} \\ $$$$\frac{\mathrm{xy}}{\mathrm{2}}\geqslant\sqrt{\mathrm{36xy}} \\ $$$$\mathrm{xy}\geqslant\mathrm{12}\sqrt{\mathrm{xy}} \\ $$$$\left(\mathrm{xy}\right)^{\mathrm{2}} \geqslant\mathrm{144xy} \\ $$$$\mathrm{xy}\left(\mathrm{xy}−\mathrm{144}\right)\geqslant\mathrm{0}\Rightarrow\mathrm{xy}\geqslant\mathrm{144} \\ $$$$ \\ $$$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{2}}\geqslant\sqrt{\mathrm{xy}}\geqslant\sqrt{\mathrm{144}}=\mathrm{12} \\ $$$$\mathrm{x}+\mathrm{y}\geqslant\mathrm{24} \\ $$$$ \\ $$

Commented by mr W last updated on 17/Jun/22

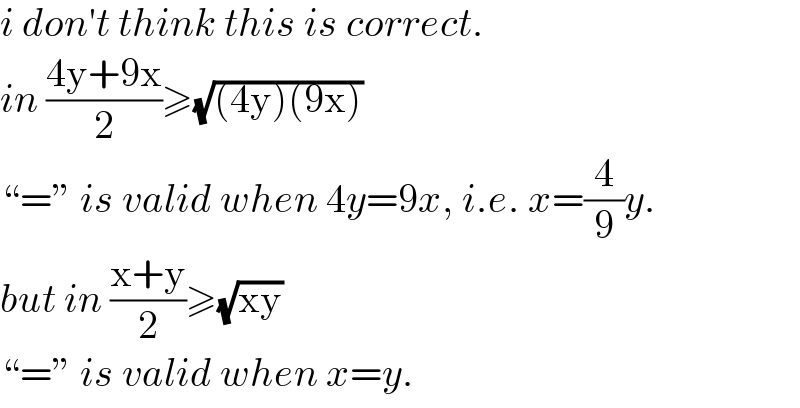
i don′t think this is correct. in ((4y+9x)/2)≥(√((4y)(9x))) “=” is valid when 4y=9x, i.e. x=(4/9)y. but in ((x+y)/2)≥(√(xy)) “=” is valid when x=y.

$${i}\:{don}'{t}\:{think}\:{this}\:{is}\:{correct}. \\ $$$${in}\:\frac{\mathrm{4y}+\mathrm{9x}}{\mathrm{2}}\geqslant\sqrt{\left(\mathrm{4y}\right)\left(\mathrm{9x}\right)} \\ $$$$“=''\:{is}\:{valid}\:{when}\:\mathrm{4}{y}=\mathrm{9}{x},\:{i}.{e}.\:{x}=\frac{\mathrm{4}}{\mathrm{9}}{y}. \\ $$$${but}\:{in}\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{2}}\geqslant\sqrt{\mathrm{xy}} \\ $$$$“=''\:{is}\:{valid}\:{when}\:{x}={y}. \\ $$

Commented by cortano1 last updated on 18/Jun/22

$$\:{the}\:{correct}\:{answer}\:{is}\:\mathrm{25} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply