Question Number 171565 by Tawa11 last updated on 17/Jun/22
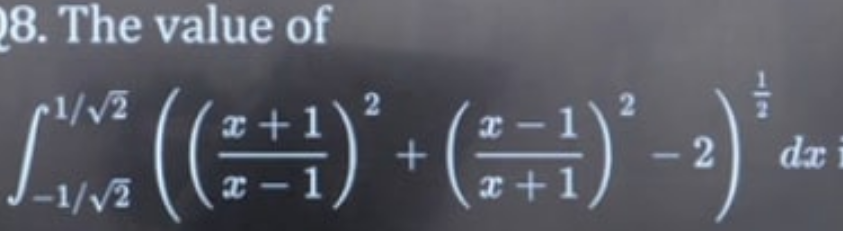
Commented by infinityaction last updated on 17/Jun/22

$$\:\:\:\:{p}\:\:=\:\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\:\:\:{then}\:\:\:\frac{\mathrm{1}}{{p}}\:\:=\:\:\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\left({p}^{\mathrm{2}} \:+\:\:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:\:−\mathrm{2}\right)^{\mathrm{1}/\mathrm{2}} =\:\:\left({p}−\frac{\mathrm{1}}{{p}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \left\{\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\:−\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} \right\}^{\mathrm{1}/\mathrm{2}} {dx} \\ $$$$\:\:\:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \left\{\left(\frac{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}+\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{x}}−\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \right\}^{\mathrm{1}/\mathrm{2}} \boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \:\left\{\left(\frac{\mathrm{4}\boldsymbol{{x}}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \right\}^{\mathrm{1}/\mathrm{2}} \boldsymbol{{dx}}\: \\ $$$$\:\:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \:\mid\frac{\mathrm{4}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\mid{dx} \\ $$$$\:\:\:\:\:\int_{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{0}} −\frac{\mathrm{4}\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}\:+\:\int_{\mathrm{0}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \frac{\mathrm{4}\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\boldsymbol{{dx}}\: \\ $$$${now}\:{complete}\:\: \\ $$
Commented by immortels last updated on 18/Jun/22

$${il}\:{y}'{a}\:{une}\:{erreur} \\ $$$$ \\ $$
Commented by infinityaction last updated on 18/Jun/22

$${where} \\ $$
Commented by immortels last updated on 19/Jun/22

$$\:\:\:\:\:\:\left({p}^{\mathrm{2}} \:+\:\:\frac{\mathrm{1}}{{p}^{\mathrm{2}} }\:\:−\mathrm{2}\right)^{\mathrm{1}/\mathrm{2}} =\:\:\left({p}−\frac{\mathrm{1}}{{p}}\right)^{\mathrm{2}} \:{ici}\:{ca}\:{dvient}\:{juste} \\ $$$$\left({p}−\frac{\mathrm{1}}{{p}}\right)\:{verifie}\:{mais}\:{apres}\:{c}.,'{est}\:{bon} \\ $$$$ \\ $$$$ \\ $$
