Question Number 171620 by mokys last updated on 18/Jun/22

Commented by mokys last updated on 18/Jun/22
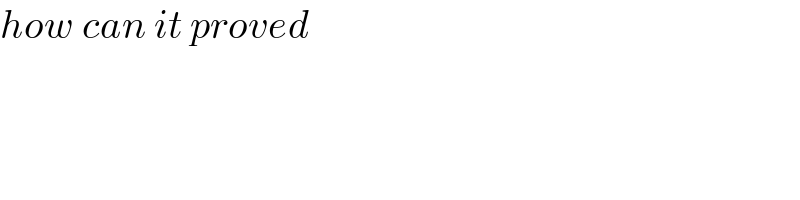
$${how}\:{can}\:{it}\:{proved} \\ $$
Commented by puissant last updated on 20/Jun/22

$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{t}^{\mathrm{2}} =\:{t}^{\mathrm{2}} \:\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\:=\:{nt}^{\mathrm{2}} . \\ $$
Commented by kaivan.ahmadi last updated on 20/Jun/22
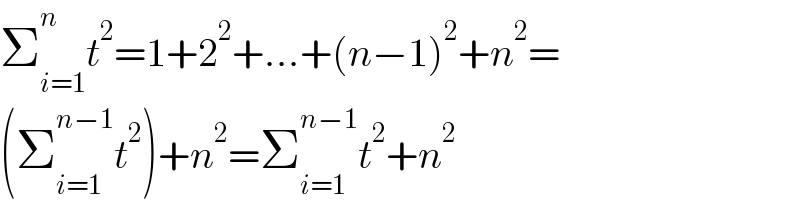
$$\sum_{{i}=\mathrm{1}} ^{{n}} {t}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}^{\mathrm{2}} +…+\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} = \\ $$$$\left(\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} {t}^{\mathrm{2}} \right)+{n}^{\mathrm{2}} =\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} {t}^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$
Commented by puissant last updated on 20/Jun/22
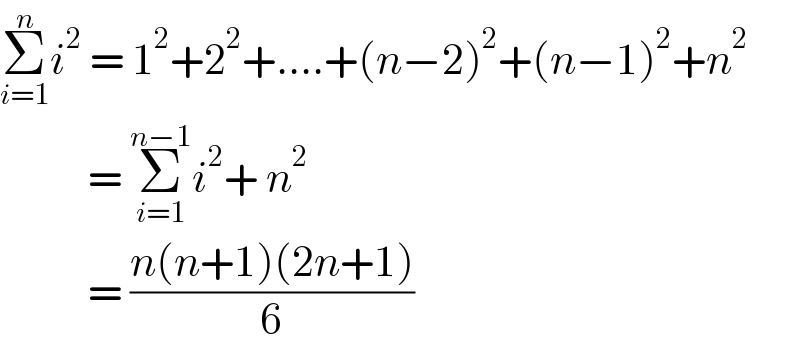
$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{i}^{\mathrm{2}} \:=\:\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +….+\left({n}−\mathrm{2}\right)^{\mathrm{2}} +\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{i}^{\mathrm{2}} +\:{n}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$
