Question Number 171667 by Mastermind last updated on 19/Jun/22

Answered by mindispower last updated on 19/Jun/22
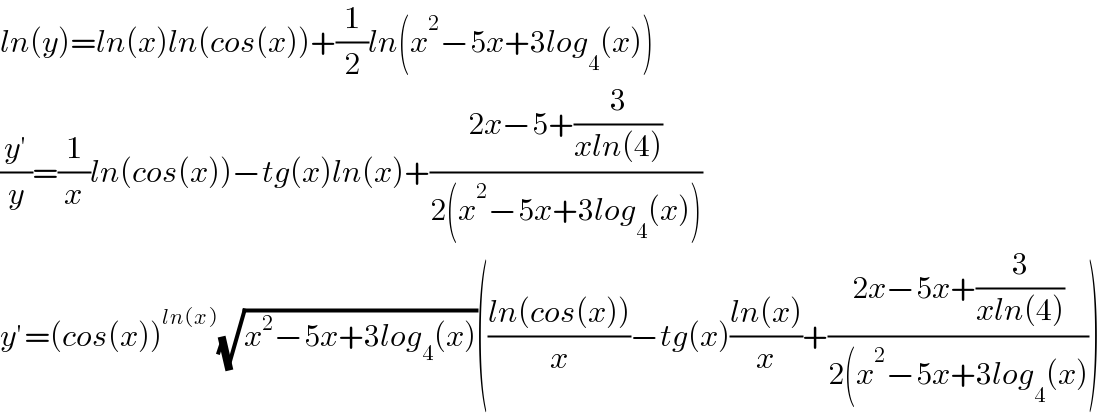
$${ln}\left({y}\right)={ln}\left({x}\right){ln}\left({cos}\left({x}\right)\right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}{log}_{\mathrm{4}} \left({x}\right)\right) \\ $$$$\frac{{y}'}{{y}}=\frac{\mathrm{1}}{{x}}{ln}\left({cos}\left({x}\right)\right)−{tg}\left({x}\right){ln}\left({x}\right)+\frac{\mathrm{2}{x}−\mathrm{5}+\frac{\mathrm{3}}{{xln}\left(\mathrm{4}\right)}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}{log}_{\mathrm{4}} \left({x}\right)\right)} \\ $$$${y}'=\left({cos}\left({x}\right)\right)^{{ln}\left({x}\right)} \sqrt{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}{log}_{\mathrm{4}} \left({x}\right)}\left(\frac{{ln}\left({cos}\left({x}\right)\right)}{{x}}−{tg}\left({x}\right)\frac{{ln}\left({x}\right)}{{x}}+\frac{\mathrm{2}{x}−\mathrm{5}{x}+\frac{\mathrm{3}}{{xln}\left(\mathrm{4}\right)}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{3}{log}_{\mathrm{4}} \left({x}\right)\right.}\right) \\ $$
