Question Number 171694 by daus last updated on 20/Jun/22

Answered by nurtani last updated on 20/Jun/22
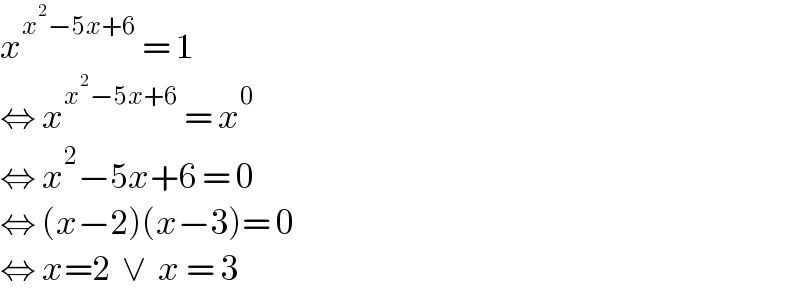
$${x}^{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}} \:=\:\mathrm{1} \\ $$$$\Leftrightarrow\:{x}^{{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}} \:=\:{x}^{\mathrm{0}} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:\left({x}−\mathrm{2}\right)\left({x}−\mathrm{3}\right)=\:\mathrm{0} \\ $$$$\Leftrightarrow\:{x}=\mathrm{2}\:\:\vee\:\:{x}\:=\:\mathrm{3} \\ $$
Answered by floor(10²Eta[1]) last updated on 20/Jun/22
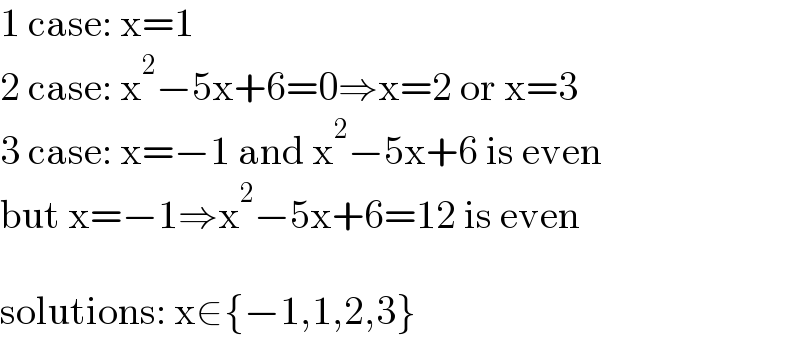
$$\mathrm{1}\:\mathrm{case}:\:\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{2}\:\mathrm{case}:\:\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}=\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{2}\:\mathrm{or}\:\mathrm{x}=\mathrm{3} \\ $$$$\mathrm{3}\:\mathrm{case}:\:\mathrm{x}=−\mathrm{1}\:\mathrm{and}\:\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}\:\mathrm{is}\:\mathrm{even} \\ $$$$\mathrm{but}\:\mathrm{x}=−\mathrm{1}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}=\mathrm{12}\:\mathrm{is}\:\mathrm{even} \\ $$$$ \\ $$$$\mathrm{solutions}:\:\mathrm{x}\in\left\{−\mathrm{1},\mathrm{1},\mathrm{2},\mathrm{3}\right\} \\ $$
