Question Number 171727 by cortano1 last updated on 20/Jun/22

Answered by mahdipoor last updated on 20/Jun/22
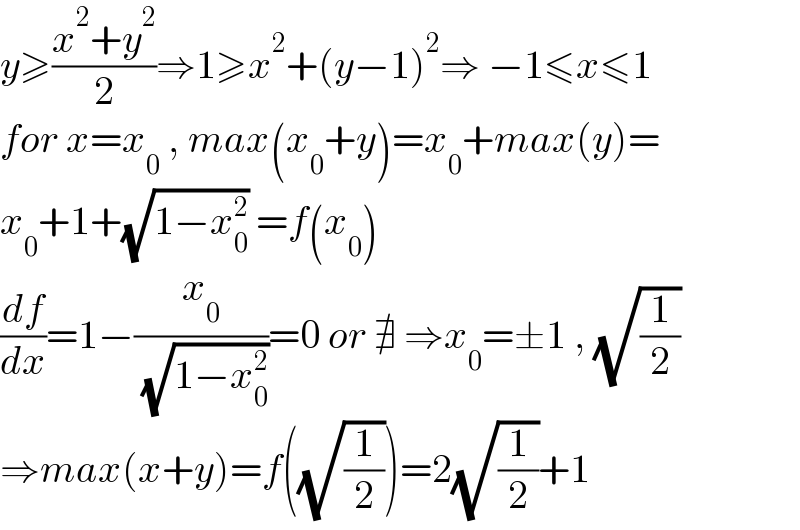
$${y}\geqslant\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}\Rightarrow\mathrm{1}\geqslant{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} \Rightarrow\:−\mathrm{1}\leqslant{x}\leqslant\mathrm{1} \\ $$$${for}\:{x}={x}_{\mathrm{0}} \:,\:{max}\left({x}_{\mathrm{0}} +{y}\right)={x}_{\mathrm{0}} +{max}\left({y}\right)= \\ $$$${x}_{\mathrm{0}} +\mathrm{1}+\sqrt{\mathrm{1}−{x}_{\mathrm{0}} ^{\mathrm{2}} }\:={f}\left({x}_{\mathrm{0}} \right) \\ $$$$\frac{{df}}{{dx}}=\mathrm{1}−\frac{{x}_{\mathrm{0}} }{\:\sqrt{\mathrm{1}−{x}_{\mathrm{0}} ^{\mathrm{2}} }}=\mathrm{0}\:{or}\:\nexists\:\Rightarrow{x}_{\mathrm{0}} =\pm\mathrm{1}\:,\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\Rightarrow{max}\left({x}+{y}\right)={f}\left(\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}\right)=\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{2}}}+\mathrm{1} \\ $$
Answered by mr W last updated on 20/Jun/22
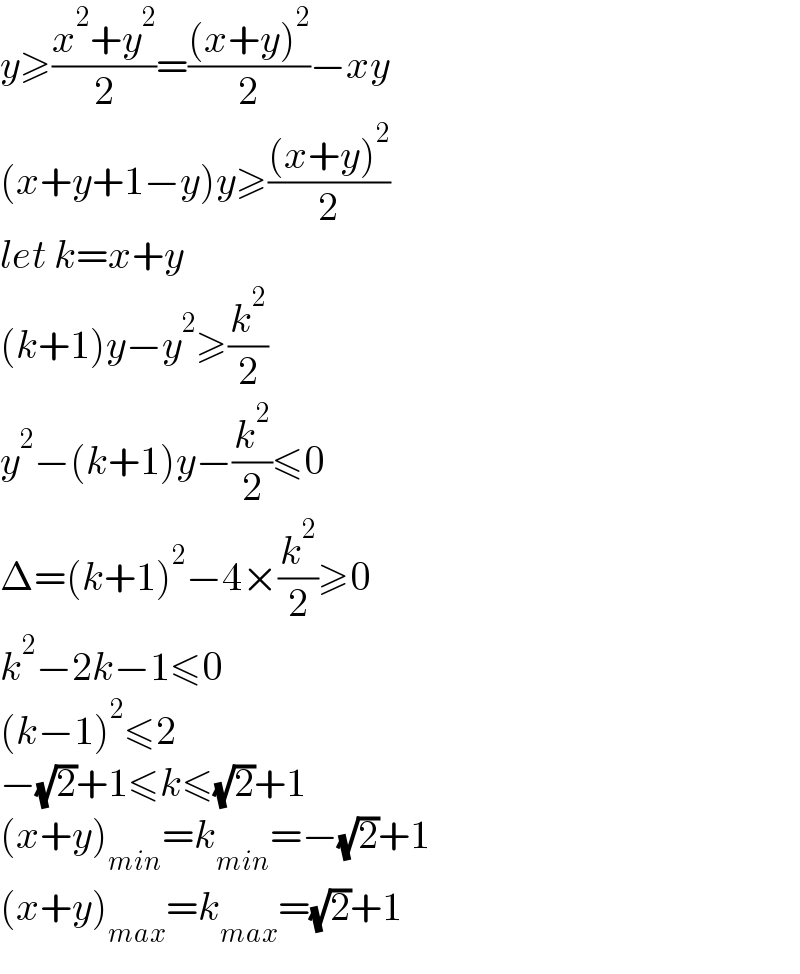
$${y}\geqslant\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}}=\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{2}}−{xy} \\ $$$$\left({x}+{y}+\mathrm{1}−{y}\right){y}\geqslant\frac{\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$${let}\:{k}={x}+{y} \\ $$$$\left({k}+\mathrm{1}\right){y}−{y}^{\mathrm{2}} \geqslant\frac{{k}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} −\left({k}+\mathrm{1}\right){y}−\frac{{k}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{0} \\ $$$$\Delta=\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4}×\frac{{k}^{\mathrm{2}} }{\mathrm{2}}\geqslant\mathrm{0} \\ $$$${k}^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\left({k}−\mathrm{1}\right)^{\mathrm{2}} \leqslant\mathrm{2} \\ $$$$−\sqrt{\mathrm{2}}+\mathrm{1}\leqslant{k}\leqslant\sqrt{\mathrm{2}}+\mathrm{1} \\ $$$$\left({x}+{y}\right)_{{min}} ={k}_{{min}} =−\sqrt{\mathrm{2}}+\mathrm{1} \\ $$$$\left({x}+{y}\right)_{{max}} ={k}_{{max}} =\sqrt{\mathrm{2}}+\mathrm{1} \\ $$
Answered by mr W last updated on 20/Jun/22
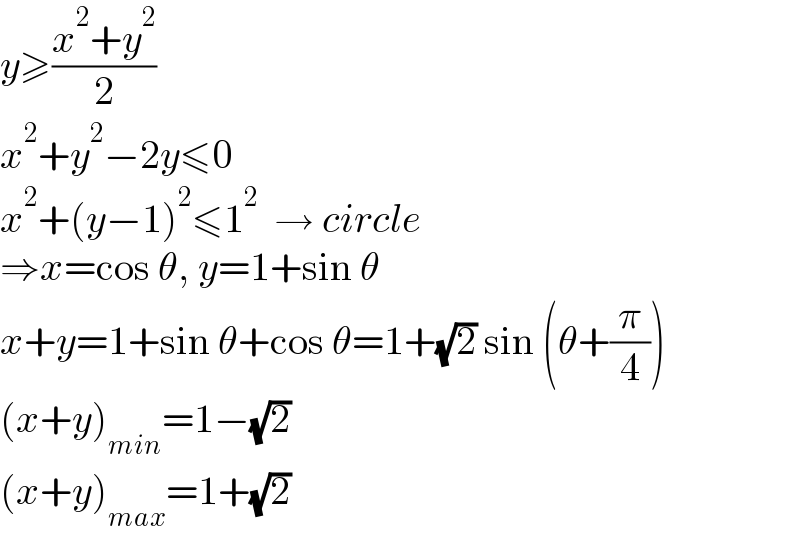
$${y}\geqslant\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{y}\leqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} \leqslant\mathrm{1}^{\mathrm{2}} \:\:\rightarrow\:{circle} \\ $$$$\Rightarrow{x}=\mathrm{cos}\:\theta,\:{y}=\mathrm{1}+\mathrm{sin}\:\theta \\ $$$${x}+{y}=\mathrm{1}+\mathrm{sin}\:\theta+\mathrm{cos}\:\theta=\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{4}}\right) \\ $$$$\left({x}+{y}\right)_{{min}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$$\left({x}+{y}\right)_{{max}} =\mathrm{1}+\sqrt{\mathrm{2}} \\ $$
