Question Number 172144 by mnjuly1970 last updated on 23/Jun/22

Answered by infinityaction last updated on 23/Jun/22

Commented by infinityaction last updated on 23/Jun/22
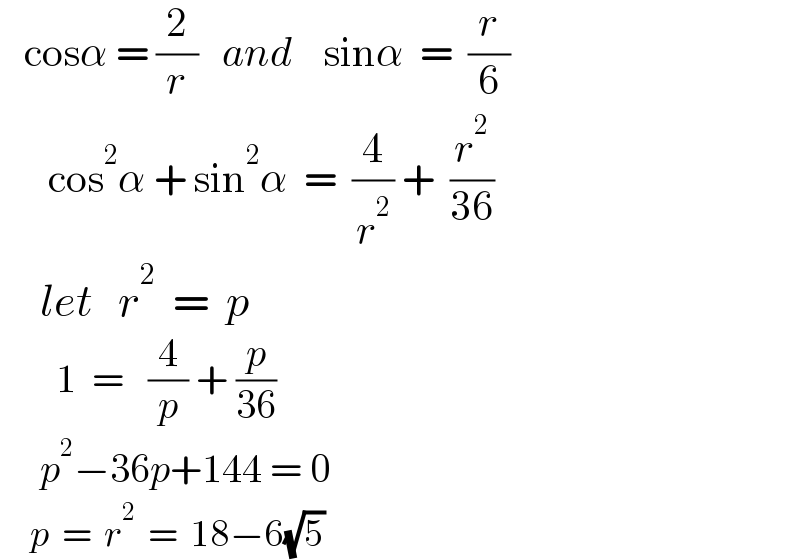
$$\:\:\:\mathrm{cos}\alpha\:=\:\frac{\mathrm{2}}{{r}}\:\:\:{and}\:\:\:\:\mathrm{sin}\alpha\:\:=\:\:\frac{{r}}{\mathrm{6}}\: \\ $$$$\:\:\:\:\:\:\mathrm{cos}^{\mathrm{2}} \alpha\:+\:\mathrm{sin}^{\mathrm{2}} \alpha\:\:=\:\:\frac{\mathrm{4}}{{r}^{\mathrm{2}} }\:+\:\:\frac{{r}^{\mathrm{2}} }{\mathrm{36}} \\ $$$$\:\:\:\:\:{let}\:\:\:{r}^{\mathrm{2}} \:\:=\:\:{p} \\ $$$$\:\:\:\:\:\:\:\mathrm{1}\:\:=\:\:\:\frac{\mathrm{4}}{{p}}\:+\:\frac{{p}}{\mathrm{36}} \\ $$$$\:\:\:\:\:{p}^{\mathrm{2}} −\mathrm{36}{p}+\mathrm{144}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:{p}\:\:=\:\:{r}^{\mathrm{2}} \:\:=\:\:\mathrm{18}−\mathrm{6}\sqrt{\mathrm{5}} \\ $$
Commented by mr W last updated on 23/Jun/22

$${nice}\:{solution}! \\ $$
Commented by mnjuly1970 last updated on 23/Jun/22
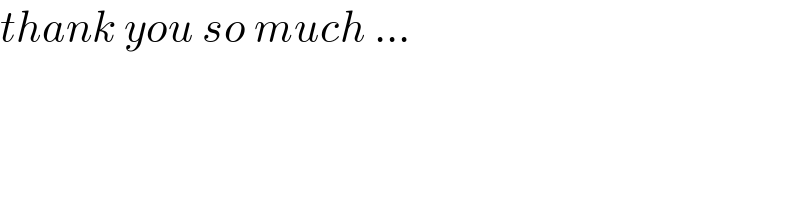
$${thank}\:{you}\:{so}\:{much}\:… \\ $$
Answered by mr W last updated on 23/Jun/22

Commented by mr W last updated on 23/Jun/22
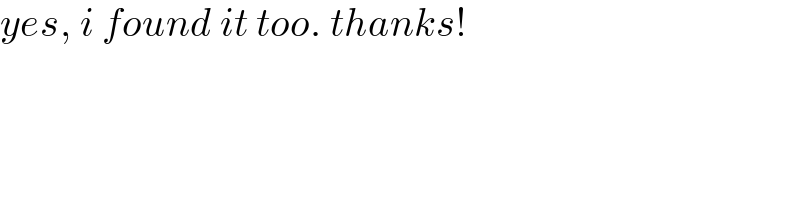
$${yes},\:{i}\:{found}\:{it}\:{too}.\:{thanks}! \\ $$
Commented by mr W last updated on 23/Jun/22

$$\gamma=\mathrm{90}°−\alpha=\mathrm{45}°+\beta \\ $$$$\frac{\mathrm{sin}\:\alpha}{{d}}=\frac{\mathrm{sin}\:\mathrm{45}°}{\mathrm{6}}\:\:\:…\left({i}\right) \\ $$$$\frac{{d}}{\mathrm{sin}\:\mathrm{45}°}=\frac{\mathrm{4}}{\mathrm{sin}\:\left(\mathrm{45}°+\beta\right)}=\frac{\mathrm{4}}{\mathrm{cos}\:\alpha}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\mathrm{45}°}=\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{45}°}{\mathrm{6}\:\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\mathrm{6}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha=\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{45}° \\ $$$$\Rightarrow\mathrm{3}\:\mathrm{sin}\:\mathrm{2}\alpha=\mathrm{2}\:\Rightarrow\mathrm{sin}\:\mathrm{2}\alpha=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\mathrm{1}=\sqrt{\mathrm{1}−\left(\frac{\mathrm{2}}{\:\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{\sqrt{\mathrm{3}+\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{6}}} \\ $$$${d}=\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{45}°}{\mathrm{cos}\:\alpha}=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}+\sqrt{\mathrm{5}}}} \\ $$$${area}\:{of}\:{square}\: \\ $$$$=\left(\frac{{d}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\frac{{d}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{8}×\mathrm{3}}{\mathrm{3}+\sqrt{\mathrm{5}}}=\mathrm{6}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right) \\ $$
Commented by mnjuly1970 last updated on 23/Jun/22

$${thanks}\:{alot}\:{sir} \\ $$
Commented by infinityaction last updated on 23/Jun/22
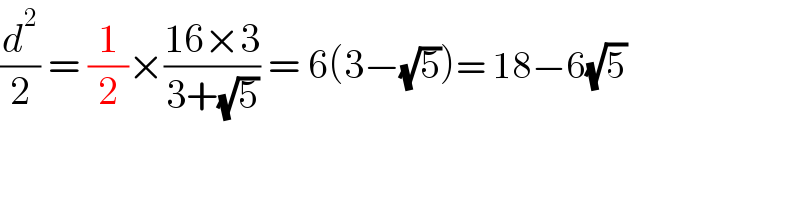
$$\frac{{d}^{\mathrm{2}} }{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{16}×\mathrm{3}}{\mathrm{3}+\sqrt{\mathrm{5}}}\:=\:\mathrm{6}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)=\:\mathrm{18}−\mathrm{6}\sqrt{\mathrm{5}} \\ $$
Commented by Tawa11 last updated on 24/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
