Question Number 172189 by Mikenice last updated on 23/Jun/22
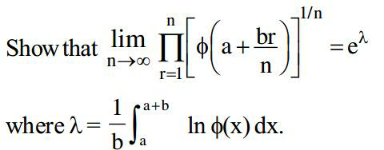
Answered by Mathspace last updated on 24/Jun/22
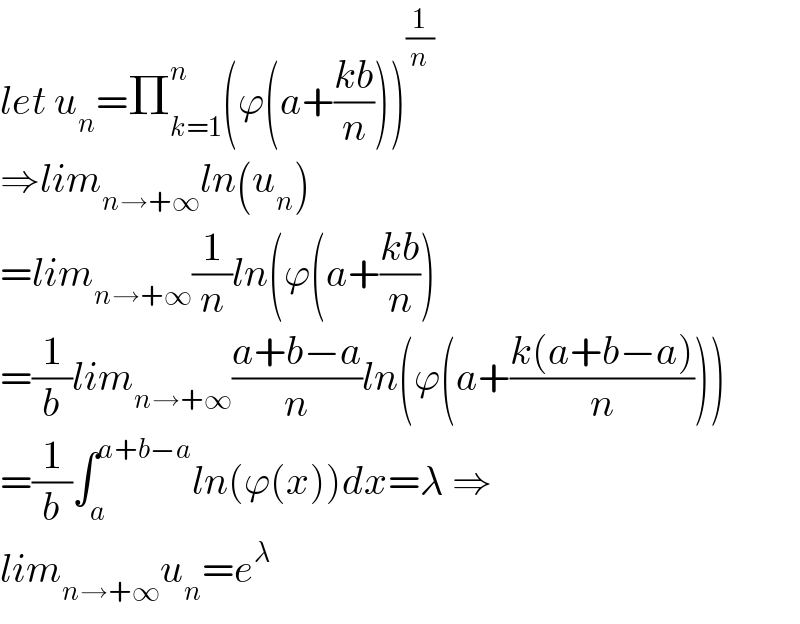
$${let}\:{u}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \left(\varphi\left({a}+\frac{{kb}}{{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow+\infty} {ln}\left({u}_{{n}} \right) \\ $$$$={lim}_{{n}\rightarrow+\infty} \frac{\mathrm{1}}{{n}}{ln}\left(\varphi\left({a}+\frac{{kb}}{{n}}\right)\right. \\ $$$$=\frac{\mathrm{1}}{{b}}{lim}_{{n}\rightarrow+\infty} \frac{{a}+{b}−{a}}{{n}}{ln}\left(\varphi\left({a}+\frac{{k}\left({a}+{b}−{a}\right)}{{n}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{b}}\int_{{a}} ^{{a}+{b}−{a}} {ln}\left(\varphi\left({x}\right)\right){dx}=\lambda\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {u}_{{n}} ={e}^{\lambda} \\ $$
