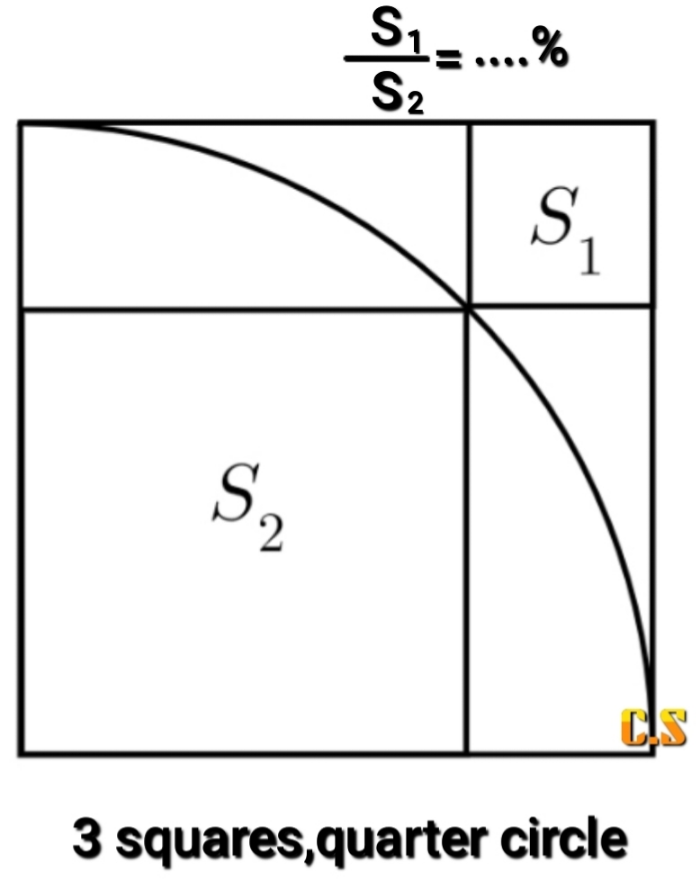
Question Number 172195 by cherokeesay last updated on 24/Jun/22
Answered by som(math1967) last updated on 24/Jun/22
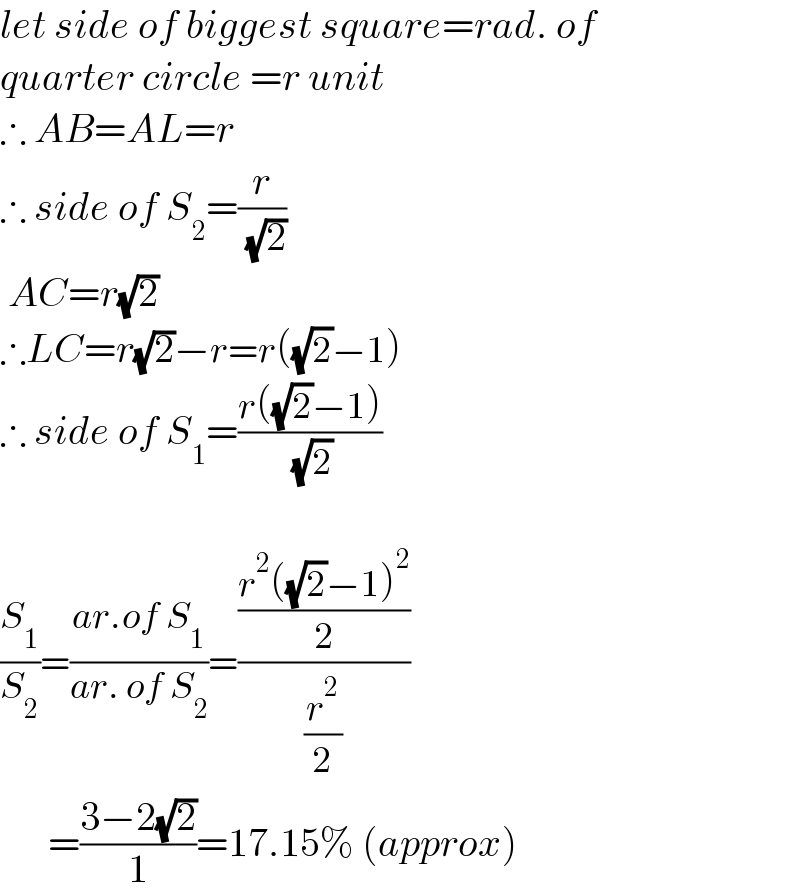
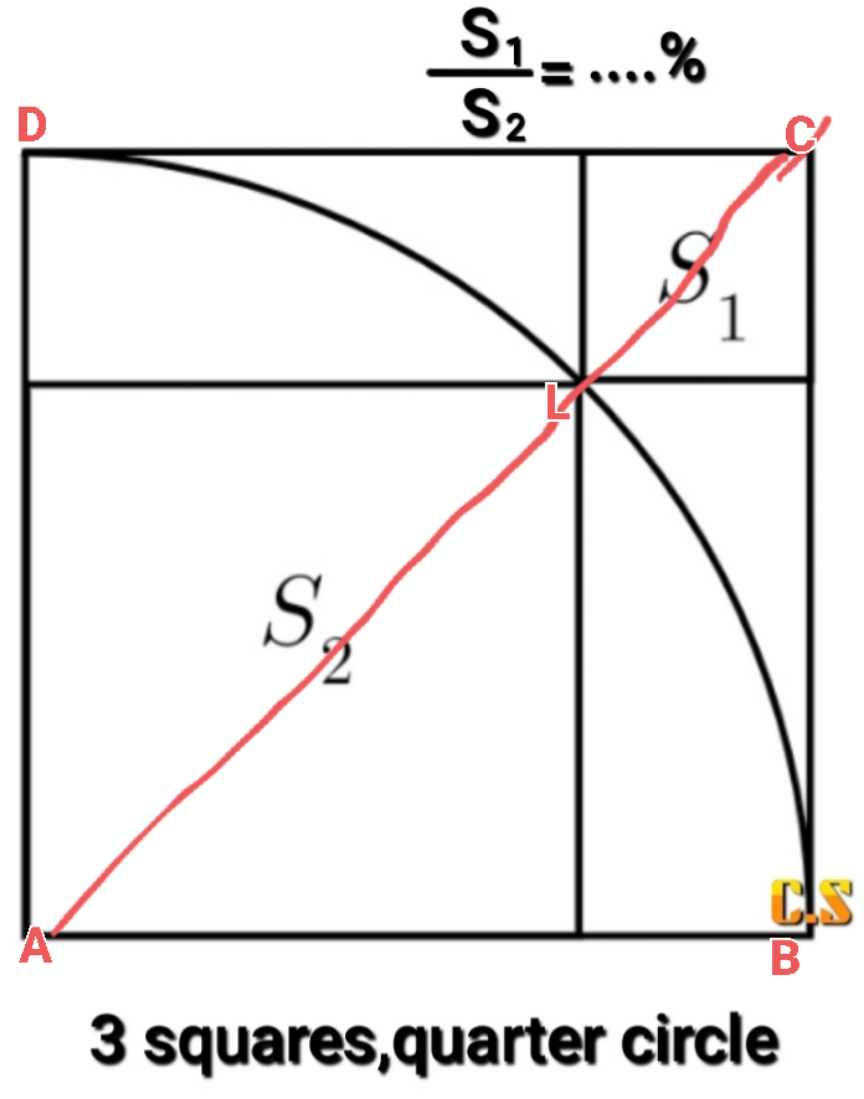
$${let}\:{side}\:{of}\:{biggest}\:{square}={rad}.\:{of} \\ $$$${quarter}\:{circle}\:={r}\:{unit} \\ $$$$\therefore\:{AB}={AL}={r} \\ $$$$\therefore\:{side}\:{of}\:{S}_{\mathrm{2}} =\frac{{r}}{\:\sqrt{\mathrm{2}}} \\ $$$$\:{AC}={r}\sqrt{\mathrm{2}} \\ $$$$\therefore{LC}={r}\sqrt{\mathrm{2}}−{r}={r}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\therefore\:{side}\:{of}\:{S}_{\mathrm{1}} =\frac{{r}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$$$\frac{{S}_{\mathrm{1}} }{{S}_{\mathrm{2}} }=\frac{{ar}.{of}\:{S}_{\mathrm{1}} }{{ar}.\:{of}\:{S}_{\mathrm{2}} }=\frac{\frac{{r}^{\mathrm{2}} \left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}}{\frac{{r}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{1}}=\mathrm{17}.\mathrm{15\%}\:\left({approx}\right) \\ $$
Commented by som(math1967) last updated on 24/Jun/22
Commented by cherokeesay last updated on 24/Jun/22

$${thank}\:{sir}\:! \\ $$
