Question-172202

Question Number 172202 by mr W last updated on 24/Jun/22

Commented by infinityaction last updated on 24/Jun/22

$$?=\:\sqrt{\frac{\mathrm{14}×\mathrm{16}}{\mathrm{14}}\:}\:\:=\:\:\mathrm{4}\: \\ $$

Answered by Rasheed.Sindhi last updated on 24/Jun/22

(?)^2 =3^2 +2^2 −2(3)(2)cos(θ)=4^2 +2^2 −2(4)(2)cos(π−θ) 9+4−12cos θ=16+4+16cos θ 28cos θ=−7 cos θ=−(1/4) ?=(√(3^2 +2^2 −2(3)(2)cos θ)) =(√(9+4−12(−(1/4)))) =(√(13+3)) =4 •Cyclic quadrilateral has its opposite angles supplementary. • cos(π−θ)=−cos θ • a^2 =b^2 +c^2 −2bc cos θ

$$\left(?\right)^{\mathrm{2}} =\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}\right)\left(\mathrm{2}\right)\mathrm{cos}\left(\theta\right)=\mathrm{4}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{4}\right)\left(\mathrm{2}\right)\mathrm{cos}\left(\pi−\theta\right)\: \\ $$$$\mathrm{9}+\mathrm{4}−\mathrm{12cos}\:\theta=\mathrm{16}+\mathrm{4}+\mathrm{16cos}\:\theta \\ $$$$\mathrm{28cos}\:\theta=−\mathrm{7} \\ $$$$\:\:\:\mathrm{cos}\:\theta=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$?=\sqrt{\mathrm{3}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}\right)\left(\mathrm{2}\right)\mathrm{cos}\:\theta} \\ $$$$\:\:\:=\sqrt{\mathrm{9}+\mathrm{4}−\mathrm{12}\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\:\:\:=\sqrt{\mathrm{13}+\mathrm{3}}\:=\mathrm{4} \\ $$$$\bullet\mathrm{Cyclic}\:\mathrm{quadrilateral}\:\mathrm{has}\:\mathrm{its}\:\mathrm{opposite} \\ $$$$\:\:\:\:\mathrm{angles}\:\mathrm{supplementary}. \\ $$$$\bullet\:\mathrm{cos}\left(\pi−\theta\right)=−\mathrm{cos}\:\theta \\ $$$$\bullet\:{a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}\:\mathrm{cos}\:\theta \\ $$

Answered by infinityaction last updated on 24/Jun/22

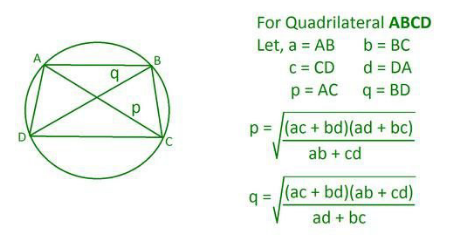
Commented by infinityaction last updated on 24/Jun/22

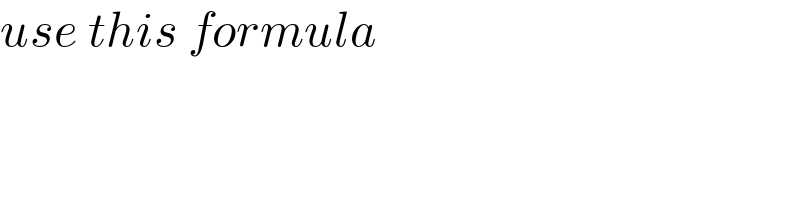
$${use}\:{this}\:{formula} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply