Question Number 172264 by Mikenice last updated on 25/Jun/22
Answered by Rasheed.Sindhi last updated on 25/Jun/22
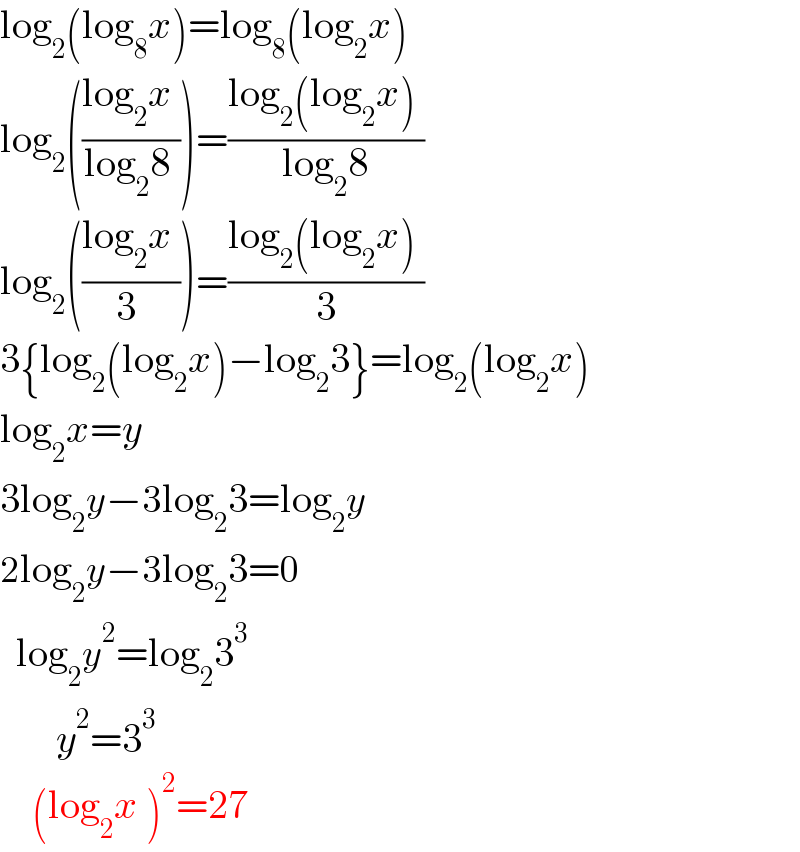
$$\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{8}} {x}\right)=\mathrm{log}_{\mathrm{8}} \left(\mathrm{log}_{\mathrm{2}} {x}\right)\:\:\:\: \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{log}_{\mathrm{2}} {x}\:}{\mathrm{log}_{\mathrm{2}} \mathrm{8}\:}\right)=\frac{\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{2}} {x}\right)\:}{\mathrm{log}_{\mathrm{2}} \mathrm{8}}\:\: \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{log}_{\mathrm{2}} {x}\:}{\mathrm{3}\:}\right)=\frac{\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{2}} {x}\right)\:}{\mathrm{3}}\:\: \\ $$$$\mathrm{3}\left\{\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{2}} {x}\right)−\mathrm{log}_{\mathrm{2}} \mathrm{3}\right\}=\mathrm{log}_{\mathrm{2}} \left(\mathrm{log}_{\mathrm{2}} {x}\right) \\ $$$$\mathrm{log}_{\mathrm{2}} {x}={y} \\ $$$$\mathrm{3log}_{\mathrm{2}} {y}−\mathrm{3log}_{\mathrm{2}} \mathrm{3}=\mathrm{log}_{\mathrm{2}} {y} \\ $$$$\mathrm{2log}_{\mathrm{2}} {y}−\mathrm{3log}_{\mathrm{2}} \mathrm{3}=\mathrm{0} \\ $$$$\:\:\mathrm{log}_{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{log}_{\mathrm{2}} \mathrm{3}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:{y}^{\mathrm{2}} =\mathrm{3}^{\mathrm{3}} \\ $$$$\:\:\:\:\left(\mathrm{log}_{\mathrm{2}} {x}\:\right)^{\mathrm{2}} =\mathrm{27} \\ $$
Commented by Tawa11 last updated on 25/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jun/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\mathrm{miss}! \\ $$
Answered by greougoury555 last updated on 25/Jun/22
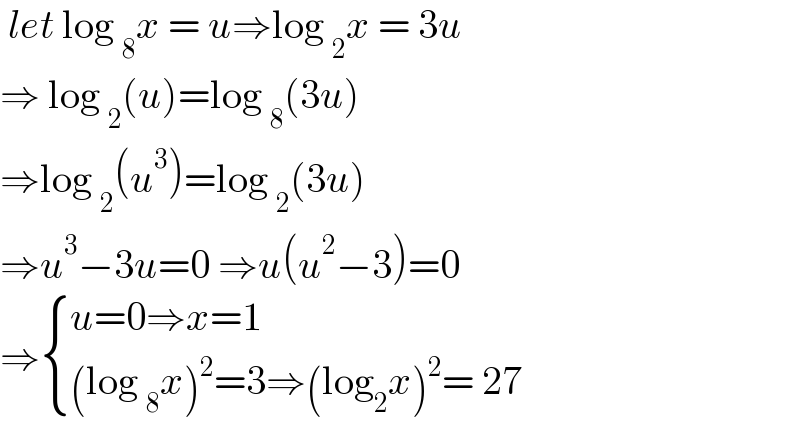
$$\:{let}\:\mathrm{log}\:_{\mathrm{8}} {x}\:=\:{u}\Rightarrow\mathrm{log}\:_{\mathrm{2}} {x}\:=\:\mathrm{3}{u} \\ $$$$\Rightarrow\:\mathrm{log}\:_{\mathrm{2}} \left({u}\right)=\mathrm{log}\:_{\mathrm{8}} \left(\mathrm{3}{u}\right) \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{2}} \left({u}^{\mathrm{3}} \right)=\mathrm{log}\:_{\mathrm{2}} \left(\mathrm{3}{u}\right) \\ $$$$\Rightarrow{u}^{\mathrm{3}} −\mathrm{3}{u}=\mathrm{0}\:\Rightarrow{u}\left({u}^{\mathrm{2}} −\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{u}=\mathrm{0}\Rightarrow{x}=\mathrm{1}}\\{\left(\mathrm{log}\:_{\mathrm{8}} {x}\right)^{\mathrm{2}} =\mathrm{3}\Rightarrow\left(\mathrm{log}_{\mathrm{2}} {x}\right)^{\mathrm{2}} =\:\mathrm{27}\:}\end{cases} \\ $$
