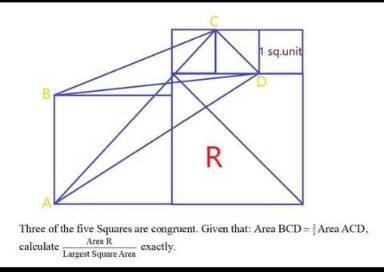
Question Number 172266 by Mikenice last updated on 25/Jun/22
Answered by mr W last updated on 25/Jun/22

Commented by mr W last updated on 25/Jun/22
![distance from B to CD =(√2)+(3/( (√2)))=(5/( (√2))) distance from A to CD =(√2)+(3/( (√2)))+(x/( (√2)))=((x+5)/( (√2))) ((area BCD)/(area ACD))=((distance from B to CD)/(distance from A to CD)) (2/3)=(5/(x+5)) ⇒x=(5/2) tan α=(3/(x+2))=(3/((5/2)+2))=(2/3) (h_1 /(tan α))+h_1 =x+3 ((3h_1 )/2)+h_1 =(5/2)+3 ⇒h_1 =((11)/5) h_2 =x tan α=(5/2)×(2/3)=(5/3) area R=(((x+3)h_1 )/2)−((xh_2 )/2) =(1/2)[((5/2)+3)((11)/5)−(5/2)×(5/3)]=((119)/(30)) area largest square=3^2 =9 ((area R)/(area largest square))=((119)/(30×9))=((119)/(270))≈44%](https://www.tinkutara.com/question/Q172280.png)
$${distance}\:{from}\:{B}\:{to}\:{CD} \\ $$$$=\sqrt{\mathrm{2}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}=\frac{\mathrm{5}}{\:\sqrt{\mathrm{2}}} \\ $$$${distance}\:{from}\:{A}\:{to}\:{CD} \\ $$$$=\sqrt{\mathrm{2}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}+\frac{{x}}{\:\sqrt{\mathrm{2}}}=\frac{{x}+\mathrm{5}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{{area}\:{BCD}}{{area}\:{ACD}}=\frac{{distance}\:{from}\:{B}\:{to}\:{CD}}{{distance}\:{from}\:{A}\:{to}\:{CD}} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{5}}{{x}+\mathrm{5}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{3}}{{x}+\mathrm{2}}=\frac{\mathrm{3}}{\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\frac{{h}_{\mathrm{1}} }{\mathrm{tan}\:\alpha}+{h}_{\mathrm{1}} ={x}+\mathrm{3} \\ $$$$\frac{\mathrm{3}{h}_{\mathrm{1}} }{\mathrm{2}}+{h}_{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3} \\ $$$$\Rightarrow{h}_{\mathrm{1}} =\frac{\mathrm{11}}{\mathrm{5}} \\ $$$${h}_{\mathrm{2}} ={x}\:\mathrm{tan}\:\alpha=\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${area}\:{R}=\frac{\left({x}+\mathrm{3}\right){h}_{\mathrm{1}} }{\mathrm{2}}−\frac{{xh}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{3}\right)\frac{\mathrm{11}}{\mathrm{5}}−\frac{\mathrm{5}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{3}}\right]=\frac{\mathrm{119}}{\mathrm{30}} \\ $$$${area}\:{largest}\:{square}=\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\frac{{area}\:{R}}{{area}\:{largest}\:{square}}=\frac{\mathrm{119}}{\mathrm{30}×\mathrm{9}}=\frac{\mathrm{119}}{\mathrm{270}}\approx\mathrm{44\%} \\ $$
Commented by Tawa11 last updated on 25/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
