Question-172284

Question Number 172284 by mnjuly1970 last updated on 25/Jun/22

Answered by mr W last updated on 25/Jun/22

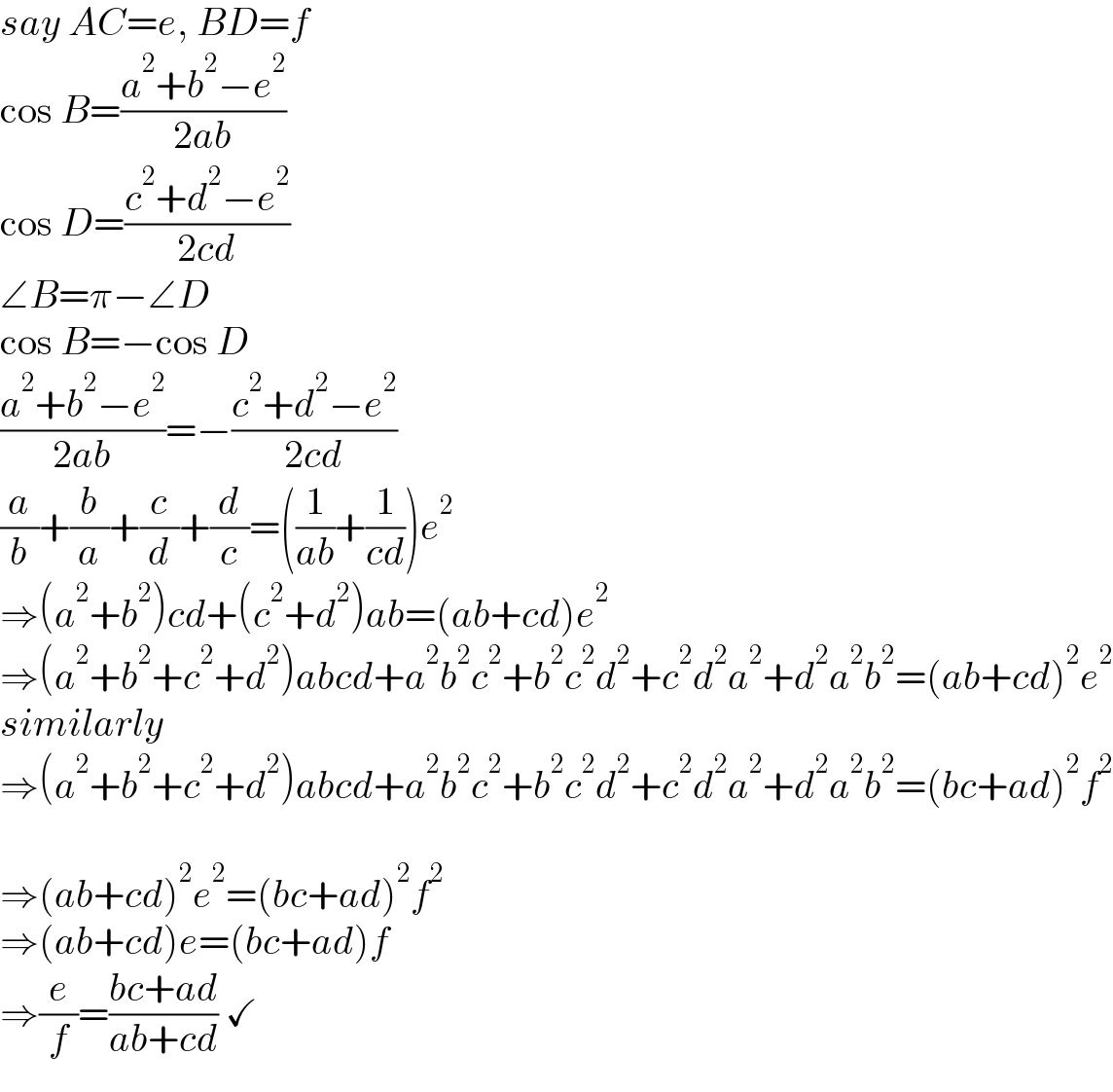
say AC=e, BD=f cos B=((a^2 +b^2 −e^2 )/(2ab)) cos D=((c^2 +d^2 −e^2 )/(2cd)) ∠B=π−∠D cos B=−cos D ((a^2 +b^2 −e^2 )/(2ab))=−((c^2 +d^2 −e^2 )/(2cd)) (a/b)+(b/a)+(c/d)+(d/c)=((1/(ab))+(1/(cd)))e^2 ⇒(a^2 +b^2 )cd+(c^2 +d^2 )ab=(ab+cd)e^2 ⇒(a^2 +b^2 +c^2 +d^2 )abcd+a^2 b^2 c^2 +b^2 c^2 d^2 +c^2 d^2 a^2 +d^2 a^2 b^2 =(ab+cd)^2 e^2 similarly ⇒(a^2 +b^2 +c^2 +d^2 )abcd+a^2 b^2 c^2 +b^2 c^2 d^2 +c^2 d^2 a^2 +d^2 a^2 b^2 =(bc+ad)^2 f^2 ⇒(ab+cd)^2 e^2 =(bc+ad)^2 f^2 ⇒(ab+cd)e=(bc+ad)f ⇒(e/f)=((bc+ad)/(ab+cd)) ✓

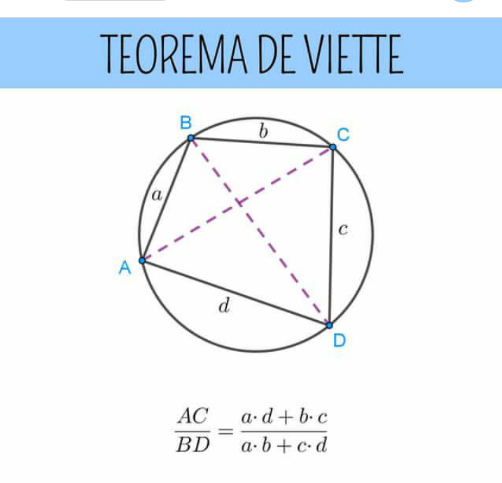
$${say}\:{AC}={e},\:{BD}={f} \\ $$$$\mathrm{cos}\:{B}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{e}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\mathrm{cos}\:{D}=\frac{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{e}^{\mathrm{2}} }{\mathrm{2}{cd}} \\ $$$$\angle{B}=\pi−\angle{D} \\ $$$$\mathrm{cos}\:{B}=−\mathrm{cos}\:{D} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{e}^{\mathrm{2}} }{\mathrm{2}{ab}}=−\frac{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} −{e}^{\mathrm{2}} }{\mathrm{2}{cd}} \\ $$$$\frac{{a}}{{b}}+\frac{{b}}{{a}}+\frac{{c}}{{d}}+\frac{{d}}{{c}}=\left(\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{cd}}\right){e}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){cd}+\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){ab}=\left({ab}+{cd}\right){e}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){abcd}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} +{c}^{\mathrm{2}} {d}^{\mathrm{2}} {a}^{\mathrm{2}} +{d}^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({ab}+{cd}\right)^{\mathrm{2}} {e}^{\mathrm{2}} \\ $$$${similarly} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right){abcd}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} {d}^{\mathrm{2}} +{c}^{\mathrm{2}} {d}^{\mathrm{2}} {a}^{\mathrm{2}} +{d}^{\mathrm{2}} {a}^{\mathrm{2}} {b}^{\mathrm{2}} =\left({bc}+{ad}\right)^{\mathrm{2}} {f}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\left({ab}+{cd}\right)^{\mathrm{2}} {e}^{\mathrm{2}} =\left({bc}+{ad}\right)^{\mathrm{2}} {f}^{\mathrm{2}} \\ $$$$\Rightarrow\left({ab}+{cd}\right){e}=\left({bc}+{ad}\right){f} \\ $$$$\Rightarrow\frac{{e}}{{f}}=\frac{{bc}+{ad}}{{ab}+{cd}}\:\checkmark \\ $$

Commented by mnjuly1970 last updated on 25/Jun/22

$$\:\:\:{thanks}\:{alot}\:\:{sir}\:{W} \\ $$

Commented by Tawa11 last updated on 25/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply