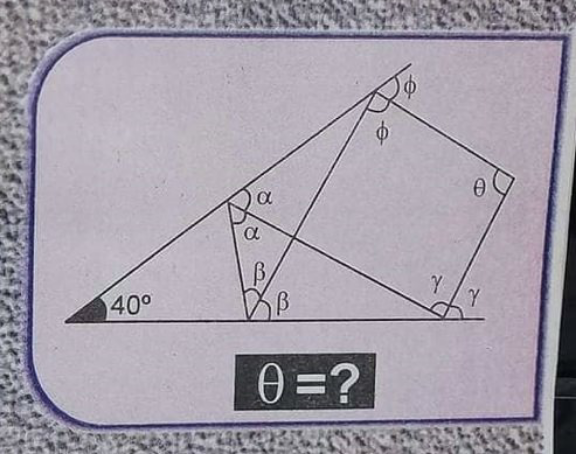
Question Number 172392 by greougoury555 last updated on 26/Jun/22
Commented by Rasheed.Sindhi last updated on 26/Jun/22

$$\theta=\mathrm{125}° \\ $$
Commented by mr W last updated on 26/Jun/22

$${yes}! \\ $$
Answered by sahiljakharjaat last updated on 26/Jun/22

Commented by som(math1967) last updated on 26/Jun/22
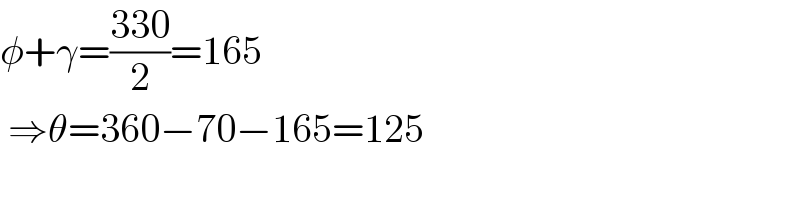
$$\phi+\gamma=\frac{\mathrm{330}}{\mathrm{2}}=\mathrm{165} \\ $$$$\:\Rightarrow\theta=\mathrm{360}−\mathrm{70}−\mathrm{165}=\mathrm{125} \\ $$
Answered by mr W last updated on 26/Jun/22

$$\mathrm{2}\alpha+\left(\mathrm{2}\beta−\mathrm{40}\right)=\mathrm{180} \\ $$$$\Rightarrow\alpha+\beta=\mathrm{110} \\ $$$$ \\ $$$$\mathrm{2}\phi+\left(\beta−\mathrm{40}\right)=\mathrm{180} \\ $$$$\Rightarrow\phi=\mathrm{110}−\frac{\beta}{\mathrm{2}} \\ $$$${similarly} \\ $$$$\Rightarrow\gamma=\mathrm{110}−\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\phi+\gamma=\mathrm{2}×\mathrm{110}−\frac{\alpha+\beta}{\mathrm{2}}=\mathrm{220}−\frac{\mathrm{110}}{\mathrm{2}}=\mathrm{165} \\ $$$$ \\ $$$$\phi+\gamma=\left(\theta_{\mathrm{1}} +\varphi_{\mathrm{1}} \right)+\left(\theta_{\mathrm{2}} +\varphi_{\mathrm{2}} \right)=\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)+\left(\varphi_{\mathrm{1}} +\varphi_{\mathrm{2}} \right)=\theta+\mathrm{40} \\ $$$$\theta+\mathrm{40}=\mathrm{165} \\ $$$$\Rightarrow\theta=\mathrm{125}\:\checkmark \\ $$
Commented by mr W last updated on 26/Jun/22

Commented by Tawa11 last updated on 26/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
