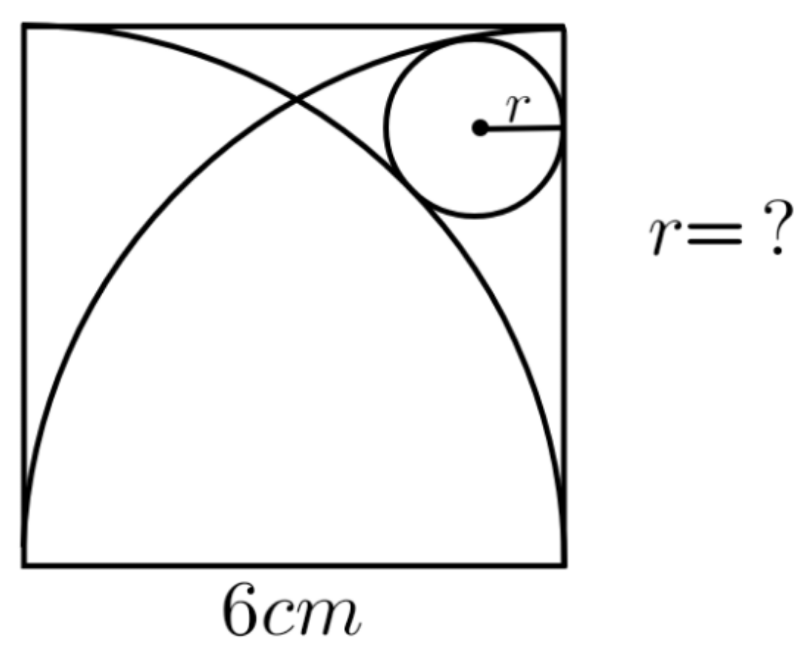
Question Number 172412 by cherokeesay last updated on 26/Jun/22
Answered by aleks041103 last updated on 26/Jun/22

$${distance}\:{from}\:{unknown}\:{center}\:{to} \\ $$$${left}\:{side}\:{is}\:{r}. \\ $$$${distance}\:{from}\:{center}\:{to}\:{top}\:{side}\:{is}\:{d}. \\ $$$$\Rightarrow\left(\mathrm{6}−{d}\right)^{\mathrm{2}} +\left(\mathrm{6}−{r}\right)^{\mathrm{2}} =\left(\mathrm{6}+{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{6}−{d}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} =\left(\mathrm{6}−{r}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{6}−{d}\right)^{\mathrm{2}} =\left(\mathrm{6}+{r}−\mathrm{6}+{r}\right)\left(\mathrm{6}+{r}+\mathrm{6}−{r}\right)= \\ $$$$=\mathrm{24}{r} \\ $$$$\left(\mathrm{6}−{d}\right)^{\mathrm{2}} =\left(\mathrm{6}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{36}−\mathrm{12}{r} \\ $$$$\Rightarrow\mathrm{36}=\mathrm{36}{r} \\ $$$$\Rightarrow{r}=\mathrm{1} \\ $$
Commented by aleks041103 last updated on 26/Jun/22
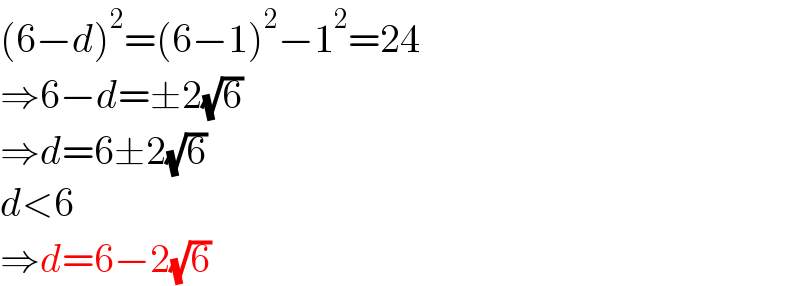
$$\left(\mathrm{6}−{d}\right)^{\mathrm{2}} =\left(\mathrm{6}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} =\mathrm{24} \\ $$$$\Rightarrow\mathrm{6}−{d}=\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\Rightarrow{d}=\mathrm{6}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$${d}<\mathrm{6} \\ $$$$\Rightarrow{d}=\mathrm{6}−\mathrm{2}\sqrt{\mathrm{6}} \\ $$
Commented by cherokeesay last updated on 26/Jun/22

$${Nice}\:!\:{thank}\:{you}. \\ $$
Commented by Tawa11 last updated on 26/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by uochiton last updated on 27/Jun/22
![(6+r)^2 =(6−r)^2 +(6−d)^2 (6+r)^2 −(6−r)^2 =(6−d)^2 [(6+r)+(6−r)]∙[(6+r)−(6−r)]=(6−d)^2 12∙2∙r=(6−d)^2 24∙r=(6−d)^2 (6−r)^2 =r^2 +(6−d)^2 (6−r)^2 =r^2 +24∙r 36−12∙r+r^2 =r^2 +24∙r 36∙r=36 r=1](https://www.tinkutara.com/question/Q172442.png)
$$\left(\mathrm{6}+{r}\right)^{\mathrm{2}} =\left(\mathrm{6}−{r}\right)^{\mathrm{2}} +\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{6}+{r}\right)^{\mathrm{2}} −\left(\mathrm{6}−{r}\right)^{\mathrm{2}} =\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{6}+{r}\right)+\left(\mathrm{6}−{r}\right)\right]\centerdot\left[\left(\mathrm{6}+{r}\right)−\left(\mathrm{6}−{r}\right)\right]=\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$\mathrm{12}\centerdot\mathrm{2}\centerdot{r}=\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$\mathrm{24}\centerdot{r}=\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{6}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\left(\mathrm{6}−{d}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{6}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} +\mathrm{24}\centerdot{r} \\ $$$$\mathrm{36}−\mathrm{12}\centerdot{r}+{r}^{\mathrm{2}} ={r}^{\mathrm{2}} +\mathrm{24}\centerdot{r} \\ $$$$\mathrm{36}\centerdot{r}=\mathrm{36} \\ $$$${r}=\mathrm{1} \\ $$
