Question-172504

Question Number 172504 by mnjuly1970 last updated on 28/Jun/22

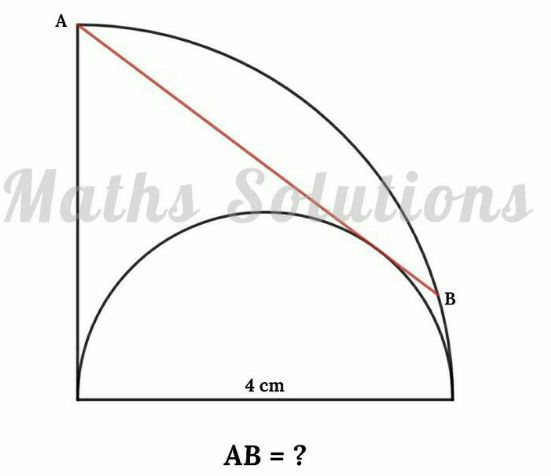
Answered by mr W last updated on 28/Jun/22

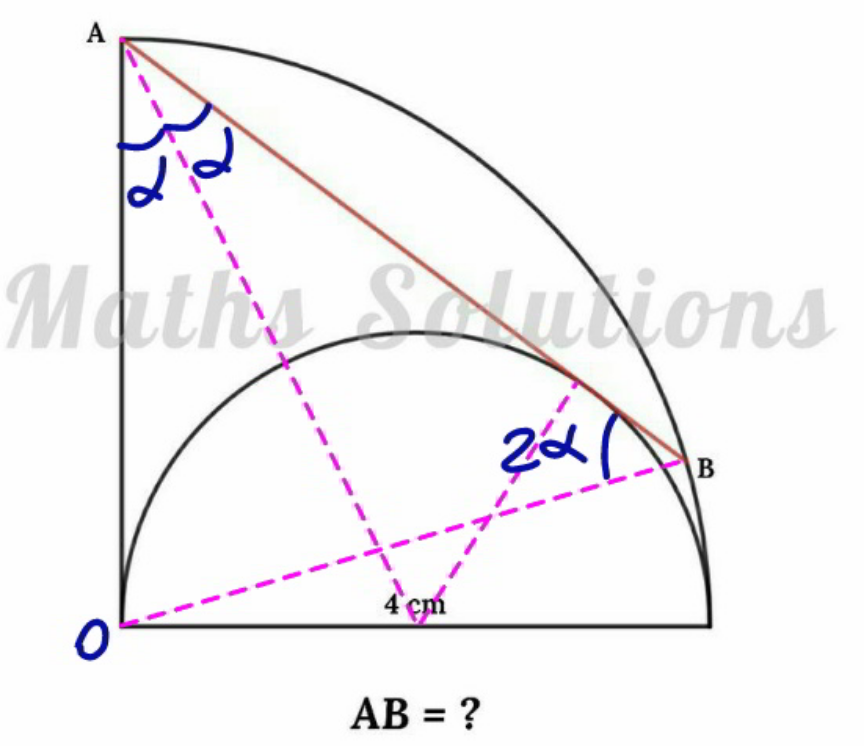
Commented by mr W last updated on 28/Jun/22

tan α=(2/4)=(1/2) ⇒sin α=(1/( (√5))) OA=OB=4 AB=2×4×cos 2α=8[1−2((1/( (√5))))^2 ]=((24)/( 5))

$$\mathrm{tan}\:\alpha=\frac{\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${OA}={OB}=\mathrm{4} \\ $$$${AB}=\mathrm{2}×\mathrm{4}×\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{8}\left[\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \right]=\frac{\mathrm{24}}{\:\mathrm{5}} \\ $$

Commented by Tawa11 last updated on 28/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by mnjuly1970 last updated on 28/Jun/22

$${grateful}\:{sir}\:{W} \\ $$

Commented by infinityaction last updated on 28/Jun/22

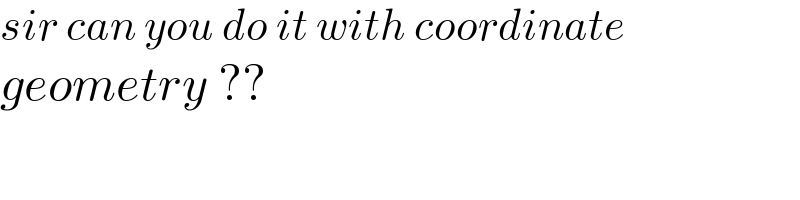
$${sir}\:{can}\:{you}\:{do}\:{it}\:{with}\:{coordinate} \\ $$$${geometry}\:?? \\ $$

Answered by mr W last updated on 28/Jun/22

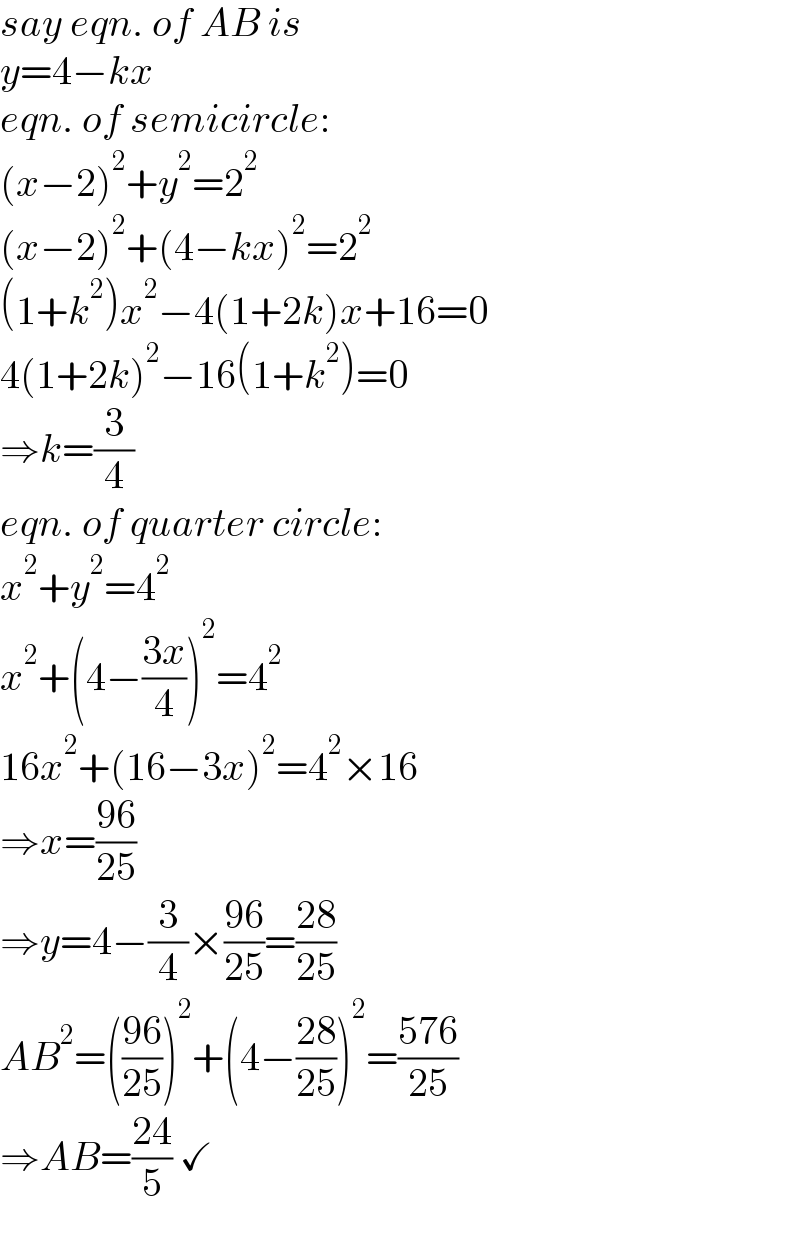
say eqn. of AB is y=4−kx eqn. of semicircle: (x−2)^2 +y^2 =2^2 (x−2)^2 +(4−kx)^2 =2^2 (1+k^2 )x^2 −4(1+2k)x+16=0 4(1+2k)^2 −16(1+k^2 )=0 ⇒k=(3/4) eqn. of quarter circle: x^2 +y^2 =4^2 x^2 +(4−((3x)/4))^2 =4^2 16x^2 +(16−3x)^2 =4^2 ×16 ⇒x=((96)/(25)) ⇒y=4−(3/4)×((96)/(25))=((28)/(25)) AB^2 =(((96)/(25)))^2 +(4−((28)/(25)))^2 =((576)/(25)) ⇒AB=((24)/5) ✓

$${say}\:{eqn}.\:{of}\:{AB}\:{is} \\ $$$${y}=\mathrm{4}−{kx} \\ $$$${eqn}.\:{of}\:{semicircle}: \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{4}−{kx}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+{k}^{\mathrm{2}} \right){x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\mathrm{2}{k}\right){x}+\mathrm{16}=\mathrm{0} \\ $$$$\mathrm{4}\left(\mathrm{1}+\mathrm{2}{k}\right)^{\mathrm{2}} −\mathrm{16}\left(\mathrm{1}+{k}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow{k}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${eqn}.\:{of}\:{quarter}\:{circle}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\left(\mathrm{4}−\frac{\mathrm{3}{x}}{\mathrm{4}}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} \\ $$$$\mathrm{16}{x}^{\mathrm{2}} +\left(\mathrm{16}−\mathrm{3}{x}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} ×\mathrm{16} \\ $$$$\Rightarrow{x}=\frac{\mathrm{96}}{\mathrm{25}} \\ $$$$\Rightarrow{y}=\mathrm{4}−\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{96}}{\mathrm{25}}=\frac{\mathrm{28}}{\mathrm{25}} \\ $$$${AB}^{\mathrm{2}} =\left(\frac{\mathrm{96}}{\mathrm{25}}\right)^{\mathrm{2}} +\left(\mathrm{4}−\frac{\mathrm{28}}{\mathrm{25}}\right)^{\mathrm{2}} =\frac{\mathrm{576}}{\mathrm{25}} \\ $$$$\Rightarrow{AB}=\frac{\mathrm{24}}{\mathrm{5}}\:\checkmark \\ $$

Commented by infinityaction last updated on 28/Jun/22