Menu Close

Question-172509

Tinku Tara 0 Comments
Pin




Question Number 172509 by Mikenice last updated on 28/Jun/22
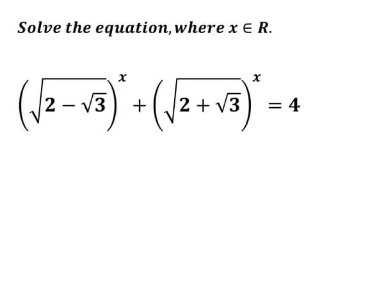
Commented by bagjagugum123 last updated on 28/Jun/22
x=2 ??
$${x}=\mathrm{2}\:?? \\ $$
Commented by Mikenice last updated on 28/Jun/22
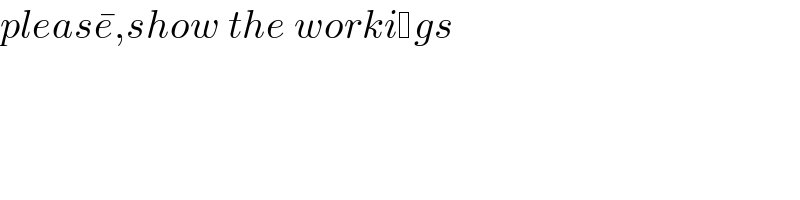
please^� ,show the worki gs
$${pleas}\bar {{e}},{show}\:{the}\:{worki} {gs} \\ $$
Answered by Rasheed.Sindhi last updated on 28/Jun/22
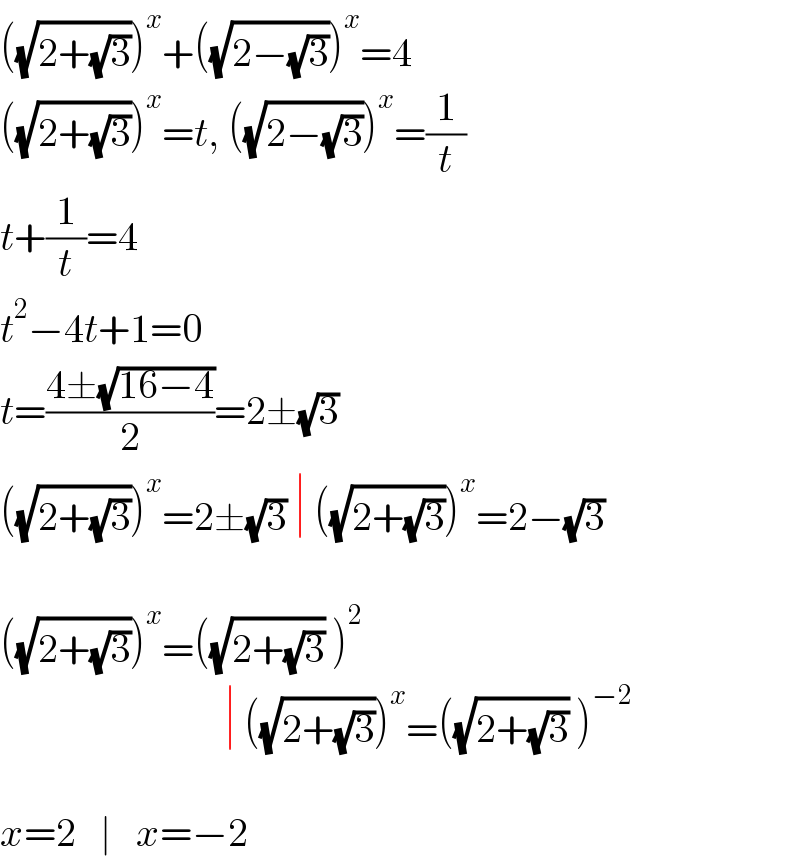
((√(2+(√3))))^x +((√(2−(√3))))^x =4 ((√(2+(√3))))^x =t, ((√(2−(√3))))^x =(1/t) t+(1/t)=4 t^2 −4t+1=0 t=((4±(√(16−4)))/2)=2±(√3) ((√(2+(√3))))^x =2±(√3) ∣ ((√(2+(√3))))^x =2−(√3) ((√(2+(√3))))^x =((√(2+(√3))) )^2 ∣ ((√(2+(√3))))^x =((√(2+(√3))) )^(−2) x=2 ∣ x=−2
$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} +\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{4} \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} ={t},\:\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{{x}} =\frac{\mathrm{1}}{{t}} \\ $$$${t}+\frac{\mathrm{1}}{{t}}=\mathrm{4} \\ $$$${t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{2}\pm\sqrt{\mathrm{3}}\:\mid\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{\mathrm{2}} \: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{−\mathrm{2}} \\ $$$$ \\ $$$${x}=\mathrm{2}\:\:\:\mid\:\:\:{x}=−\mathrm{2} \\ $$
Answered by Mathspace last updated on 28/Jun/22
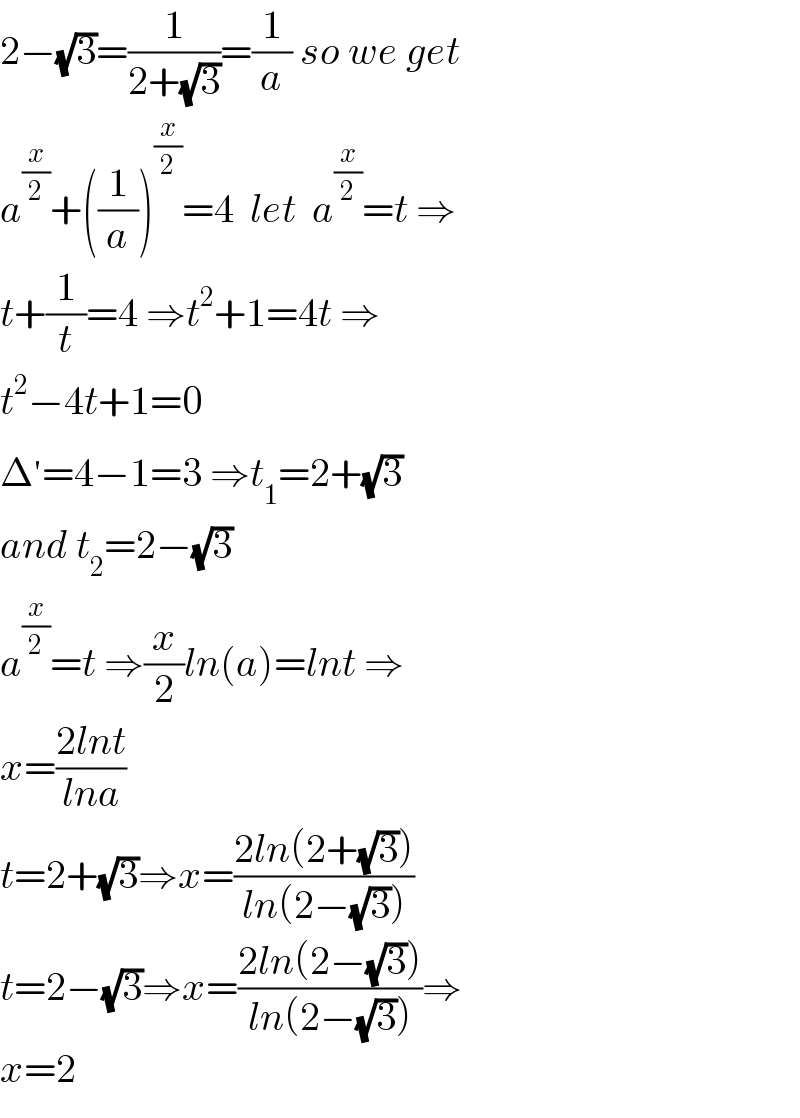
2−(√3)=(1/(2+(√3)))=(1/a) so we get a^(x/2) +((1/a))^(x/2) =4 let a^(x/2) =t ⇒ t+(1/t)=4 ⇒t^2 +1=4t ⇒ t^2 −4t+1=0 Δ^′ =4−1=3 ⇒t_1 =2+(√3) and t_2 =2−(√3) a^(x/2) =t ⇒(x/2)ln(a)=lnt ⇒ x=((2lnt)/(lna)) t=2+(√3)⇒x=((2ln(2+(√3)))/(ln(2−(√3)))) t=2−(√3)⇒x=((2ln(2−(√3)))/(ln(2−(√3))))⇒ x=2
$$\mathrm{2}−\sqrt{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}=\frac{\mathrm{1}}{{a}}\:{so}\:{we}\:{get} \\ $$$${a}^{\frac{{x}}{\mathrm{2}}} +\left(\frac{\mathrm{1}}{{a}}\right)^{\frac{{x}}{\mathrm{2}}} =\mathrm{4}\:\:{let}\:\:{a}^{\frac{{x}}{\mathrm{2}}} ={t}\:\Rightarrow \\ $$$${t}+\frac{\mathrm{1}}{{t}}=\mathrm{4}\:\Rightarrow{t}^{\mathrm{2}} +\mathrm{1}=\mathrm{4}{t}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta^{'} =\mathrm{4}−\mathrm{1}=\mathrm{3}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$${and}\:{t}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${a}^{\frac{{x}}{\mathrm{2}}} ={t}\:\Rightarrow\frac{{x}}{\mathrm{2}}{ln}\left({a}\right)={lnt}\:\Rightarrow \\ $$$${x}=\frac{\mathrm{2}{lnt}}{{lna}} \\ $$$${t}=\mathrm{2}+\sqrt{\mathrm{3}}\Rightarrow{x}=\frac{\mathrm{2}{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{{ln}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$${t}=\mathrm{2}−\sqrt{\mathrm{3}}\Rightarrow{x}=\frac{\mathrm{2}{ln}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{{ln}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}\Rightarrow \\ $$$${x}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *