Question-172531

Facebook Tweet Pin

Question Number 172531 by Mikenice last updated on 28/Jun/22

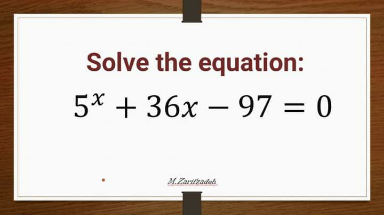
Commented by GalaxyBills last updated on 29/Jun/22

$$ \\ $$

Answered by MJS_new last updated on 28/Jun/22

$${x}=\mathrm{2} \\ $$

Commented by Mikenice last updated on 28/Jun/22

$${please}\:{show}\:{the}\:{workings} \\ $$

Commented by MJS_new last updated on 28/Jun/22

for obvious solutions: no workings, just used my brain. for approximate solutions: just used a good calculator

$$\mathrm{for}\:\mathrm{obvious}\:\mathrm{solutions}:\:\mathrm{no}\:\mathrm{workings},\:\mathrm{just}\:\mathrm{used} \\ $$$$\mathrm{my}\:\mathrm{brain}. \\ $$$$\mathrm{for}\:\mathrm{approximate}\:\mathrm{solutions}:\:\mathrm{just}\:\mathrm{used}\:\mathrm{a}\:\mathrm{good} \\ $$$$\mathrm{calculator} \\ $$

Answered by mr W last updated on 28/Jun/22

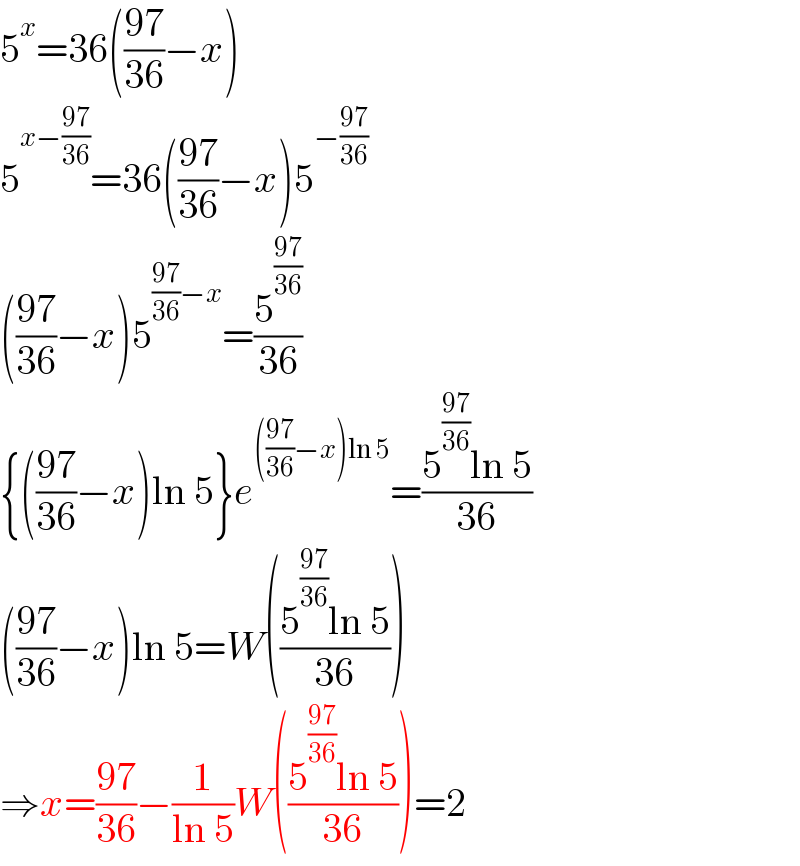
5^x =36(((97)/(36))−x) 5^(x−((97)/(36))) =36(((97)/(36))−x)5^(−((97)/(36))) (((97)/(36))−x)5^(((97)/(36))−x) =(5^((97)/(36)) /(36)) {(((97)/(36))−x)ln 5}e^((((97)/(36))−x)ln 5) =((5^((97)/(36)) ln 5)/(36)) (((97)/(36))−x)ln 5=W(((5^((97)/(36)) ln 5)/(36))) ⇒x=((97)/(36))−(1/(ln 5))W(((5^((97)/(36)) ln 5)/(36)))=2

$$\mathrm{5}^{{x}} =\mathrm{36}\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right) \\ $$$$\mathrm{5}^{{x}−\frac{\mathrm{97}}{\mathrm{36}}} =\mathrm{36}\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right)\mathrm{5}^{−\frac{\mathrm{97}}{\mathrm{36}}} \\ $$$$\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right)\mathrm{5}^{\frac{\mathrm{97}}{\mathrm{36}}−{x}} =\frac{\mathrm{5}^{\frac{\mathrm{97}}{\mathrm{36}}} }{\mathrm{36}} \\ $$$$\left\{\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right)\mathrm{ln}\:\mathrm{5}\right\}{e}^{\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right)\mathrm{ln}\:\mathrm{5}} =\frac{\mathrm{5}^{\frac{\mathrm{97}}{\mathrm{36}}} \mathrm{ln}\:\mathrm{5}}{\mathrm{36}} \\ $$$$\left(\frac{\mathrm{97}}{\mathrm{36}}−{x}\right)\mathrm{ln}\:\mathrm{5}={W}\left(\frac{\mathrm{5}^{\frac{\mathrm{97}}{\mathrm{36}}} \mathrm{ln}\:\mathrm{5}}{\mathrm{36}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{97}}{\mathrm{36}}−\frac{\mathrm{1}}{\mathrm{ln}\:\mathrm{5}}{W}\left(\frac{\mathrm{5}^{\frac{\mathrm{97}}{\mathrm{36}}} \mathrm{ln}\:\mathrm{5}}{\mathrm{36}}\right)=\mathrm{2} \\ $$

Commented by Tawa11 last updated on 30/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by GalaxyBills last updated on 29/Jun/22

$$ \\ $$Supposing x = z

5ᶻ + 36z = 97

5ᶻ + 36z= 25 + 72

By comparing

5ᶻ = 5²
z = 2

also,
36z = 72
z = 2

Hence x=2

this is given one value of x♨️🤲

Commented by mr W last updated on 29/Jun/22

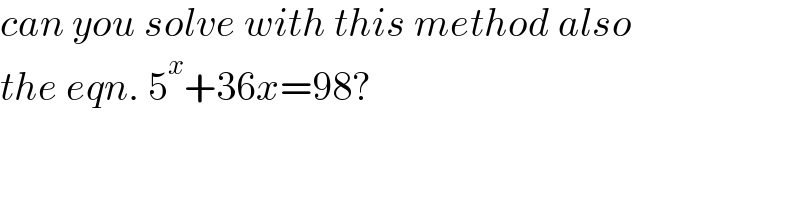
can you solve with this method also the eqn. 5^x +36x=98?

$${can}\:{you}\:{solve}\:{with}\:{this}\:{method}\:{also} \\ $$$${the}\:{eqn}.\:\mathrm{5}^{{x}} +\mathrm{36}{x}=\mathrm{98}? \\ $$

Answered by GalaxyBills last updated on 29/Jun/22

$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply