Question Number 172692 by mnjuly1970 last updated on 30/Jun/22
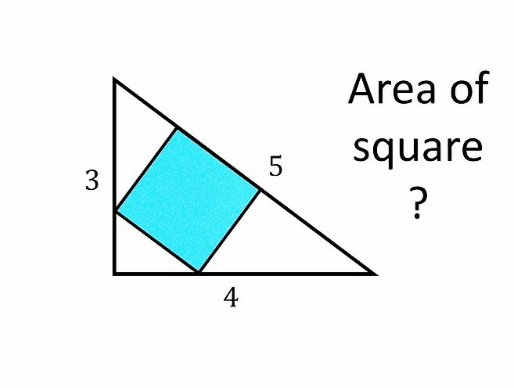
Answered by som(math1967) last updated on 30/Jun/22

Commented by som(math1967) last updated on 30/Jun/22
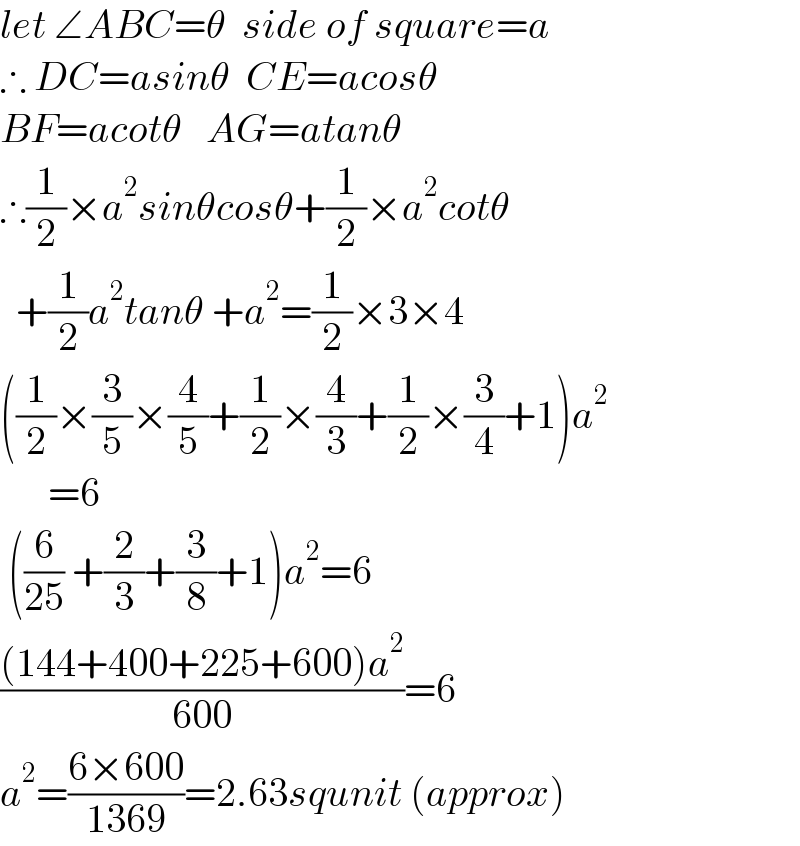
$${let}\:\angle{ABC}=\theta\:\:{side}\:{of}\:{square}={a} \\ $$$$\therefore\:{DC}={asin}\theta\:\:{CE}={acos}\theta \\ $$$${BF}={acot}\theta\:\:\:{AG}={atan}\theta \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{2}}×{a}^{\mathrm{2}} {sin}\theta{cos}\theta+\frac{\mathrm{1}}{\mathrm{2}}×{a}^{\mathrm{2}} {cot}\theta \\ $$$$\:\:+\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} {tan}\theta\:+{a}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{3}×\mathrm{4} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{4}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}\right){a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\mathrm{6} \\ $$$$\:\left(\frac{\mathrm{6}}{\mathrm{25}}\:+\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{3}}{\mathrm{8}}+\mathrm{1}\right){a}^{\mathrm{2}} =\mathrm{6} \\ $$$$\frac{\left(\mathrm{144}+\mathrm{400}+\mathrm{225}+\mathrm{600}\right){a}^{\mathrm{2}} }{\mathrm{600}}=\mathrm{6} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{6}×\mathrm{600}}{\mathrm{1369}}=\mathrm{2}.\mathrm{63}{squnit}\:\left({approx}\right) \\ $$
Commented by mnjuly1970 last updated on 30/Jun/22

$$\mathrm{tayeballah}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 30/Jun/22
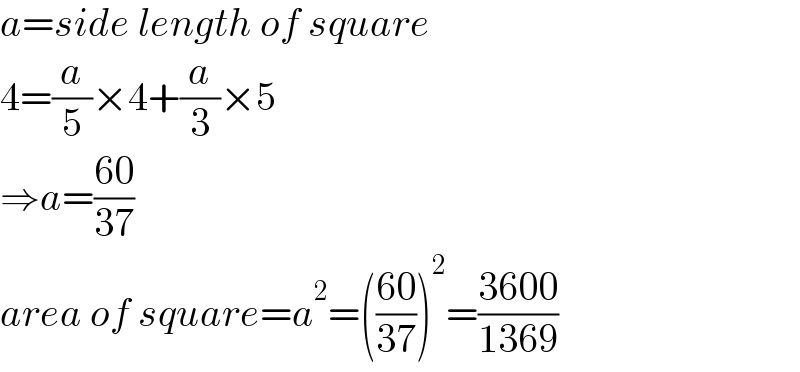
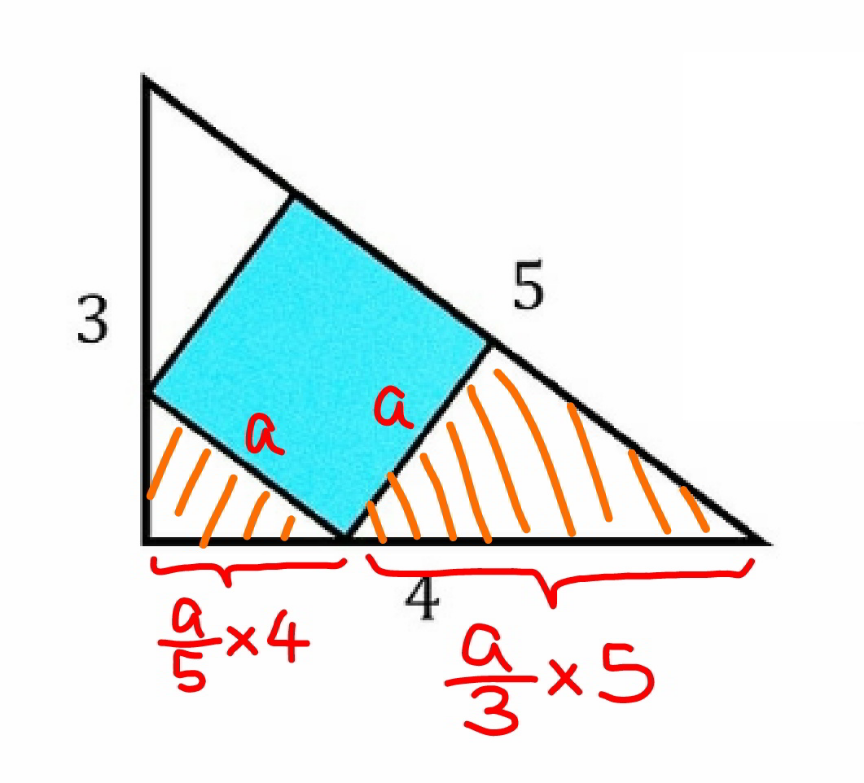
$${a}={side}\:{length}\:{of}\:{square} \\ $$$$\mathrm{4}=\frac{{a}}{\mathrm{5}}×\mathrm{4}+\frac{{a}}{\mathrm{3}}×\mathrm{5} \\ $$$$\Rightarrow{a}=\frac{\mathrm{60}}{\mathrm{37}} \\ $$$${area}\:{of}\:{square}={a}^{\mathrm{2}} =\left(\frac{\mathrm{60}}{\mathrm{37}}\right)^{\mathrm{2}} =\frac{\mathrm{3600}}{\mathrm{1369}} \\ $$
Commented by mr W last updated on 30/Jun/22
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
