Menu Close

Question-172749

Tinku Tara 0 Comments
Pin




Question Number 172749 by saly last updated on 01/Jul/22
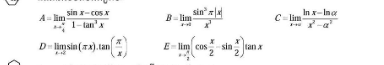
Commented by saly last updated on 01/Jul/22
Hepl me C,D,E
$$\:\:\:\:\:\:{Hepl}\:{me}\:\:{C},{D},{E} \\ $$
Commented by kaivan.ahmadi last updated on 01/Jul/22
C lim_(x→α) ((lnx−lnα)/(x^2 −α^2 ))∼lim_(x→α) ((1/x)/(2x))=(1/(2α^2 ))
$${C} \\ $$$${li}\underset{{x}\rightarrow\alpha} {{m}}\:\frac{{lnx}−{ln}\alpha}{{x}^{\mathrm{2}} −\alpha^{\mathrm{2}} }\sim{li}\underset{{x}\rightarrow\alpha} {{m}}\frac{\frac{\mathrm{1}}{{x}}}{\mathrm{2}{x}}=\frac{\mathrm{1}}{\mathrm{2}\alpha^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by saly last updated on 01/Jul/22
Thank you
$${Thank}\:{you} \\ $$
Answered by greougoury555 last updated on 01/Jul/22
⇒A=lim_(x→(π/4)) ((cos^3 x(sin x−cos x))/(cos^3 x−sin^3 x)) A=lim_(x→(π/4)) ((−cos^3 x)/(1+(1/2)sin 2x)) = −(1/(2(√2))) ×(2/3) = =−(1/(3(√2))) =−((√2)/(12))
$$\:\Rightarrow{A}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{3}} {x}\left(\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right)}{\mathrm{cos}\:^{\mathrm{3}} {x}−\mathrm{sin}\:^{\mathrm{3}} {x}} \\ $$$$\:\:\:\:\:{A}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{4}}} {\mathrm{lim}}\:\frac{−\mathrm{cos}\:^{\mathrm{3}} {x}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}} \\ $$$$\:\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:×\frac{\mathrm{2}}{\mathrm{3}}\:=\:=−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{2}}}\:=−\frac{\sqrt{\mathrm{2}}}{\mathrm{12}} \\ $$
Answered by greougoury555 last updated on 01/Jul/22
E=lim_(x→(π/2)) (cos (x/2)−sin (x/2)).tan x E=lim_(x→(π/2)) ((sin x(cos (x/2)−sin (x/2)))/((cos (x/2)−sin (x/2))(cos (x/2)+sin (x/2)))) E=(1/((1/( (√2)))+(1/( (√2))))) = (√2)
$${E}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right).\mathrm{tan}\:{x} \\ $$$${E}=\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)}{\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)} \\ $$$${E}=\frac{\mathrm{1}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\:\sqrt{\mathrm{2}}\: \\ $$
Commented by saly last updated on 01/Jul/22
Thank you
$${Thank}\:\:{you} \\ $$
Answered by Mathspace last updated on 01/Jul/22
d) f(x)=sin(πx)tan((π/x)) (x→2) (π/x)=t ⇒x=(π/t) ⇒ f(x)=sin((π^2 /t))tan(t)(t→(π/2)) let t=(π/2)−u ⇒ f(x)=sin((π^2 /((π/2)−u)))×(1/(tanu))(u→0) we have (π^2 /((π/2)−u))=((2π^2 )/(π−2u)) =((2π)/(1−((2u)/π)))∼2π(1+((2u)/π))=2π+4u⇒ sin((π^2 /((π/2)−u)))∼sin(4u)∼4u ⇒ f(x)∼4u×(1/u)=4 ⇒ lim_(x→2) f(x)=4
$$\left.{d}\right)\:{f}\left({x}\right)={sin}\left(\pi{x}\right){tan}\left(\frac{\pi}{{x}}\right)\:\:\left({x}\rightarrow\mathrm{2}\right) \\ $$$$\frac{\pi}{{x}}={t}\:\Rightarrow{x}=\frac{\pi}{{t}}\:\Rightarrow \\ $$$${f}\left({x}\right)={sin}\left(\frac{\pi^{\mathrm{2}} }{{t}}\right){tan}\left({t}\right)\left({t}\rightarrow\frac{\pi}{\mathrm{2}}\right) \\ $$$${let}\:{t}=\frac{\pi}{\mathrm{2}}−{u}\:\Rightarrow \\ $$$${f}\left({x}\right)={sin}\left(\frac{\pi^{\mathrm{2}} }{\frac{\pi}{\mathrm{2}}−{u}}\right)×\frac{\mathrm{1}}{{tanu}}\left({u}\rightarrow\mathrm{0}\right) \\ $$$${we}\:{have}\:\frac{\pi^{\mathrm{2}} }{\frac{\pi}{\mathrm{2}}−{u}}=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\pi−\mathrm{2}{u}} \\ $$$$=\frac{\mathrm{2}\pi}{\mathrm{1}−\frac{\mathrm{2}{u}}{\pi}}\sim\mathrm{2}\pi\left(\mathrm{1}+\frac{\mathrm{2}{u}}{\pi}\right)=\mathrm{2}\pi+\mathrm{4}{u}\Rightarrow \\ $$$${sin}\left(\frac{\pi^{\mathrm{2}} }{\frac{\pi}{\mathrm{2}}−{u}}\right)\sim{sin}\left(\mathrm{4}{u}\right)\sim\mathrm{4}{u}\:\Rightarrow \\ $$$${f}\left({x}\right)\sim\mathrm{4}{u}×\frac{\mathrm{1}}{{u}}=\mathrm{4}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \:{f}\left({x}\right)=\mathrm{4} \\ $$
Answered by CElcedricjunior last updated on 01/Jul/22
1)lim_(x→𝛑/4) ((sinx−cosx)/(1−tan^3 x))=(0/0)=fi =lim_( x →𝛑/4) ((cosx+sinx)/(−3(1+tan^2 x)tan^2 x)) =((√2)/(−3(2)))=−((√2)/6) 2)lim_(x→0) ((sin^3 (𝛑∣x∣))/x^3 )=±𝛑 3)lim_(x→a) ((lnx−lna)/(x^2 −a_ ^2 ))=lim_(x→a) (1/((x+a)))×((lnx−lna)/((x−a))) =(1/(2a))×(1/a)=(1/(2a^2 )) 4)lim_(x→2) sin(𝛑x).tan((𝛑/x))=0×∞=FI =lim_(x→2) cos((𝛑/2)−𝛑x)tan((𝛑/x)) posons (𝛑/2)−x𝛑=X=>x=((𝛑−2X)/(2𝛑)) qd:x→2;X→(𝛑/2) =lim_(X→(𝛑/2)) cosX.tan(((2𝛑^2 )/(𝛑−2X)))=0×0=0 5)lim_(x→(𝛑/2)) (cos(x/2)−sin(x/2))tanx=0×∞=FI =0
$$\left.\mathrm{1}\right)\underset{{x}\rightarrow\boldsymbol{\pi}/\mathrm{4}} {\mathrm{lim}}\frac{\boldsymbol{{sinx}}−\boldsymbol{{cosx}}}{\mathrm{1}−\boldsymbol{{tan}}^{\mathrm{3}} \boldsymbol{{x}}}=\frac{\mathrm{0}}{\mathrm{0}}=\boldsymbol{{fi}} \\ $$$$=\underset{\:\:\:{x}\:\:\rightarrow\boldsymbol{\pi}/\mathrm{4}} {\mathrm{lim}}\frac{\boldsymbol{{cosx}}+\boldsymbol{{sinx}}}{−\mathrm{3}\left(\mathrm{1}+\boldsymbol{{tan}}^{\mathrm{2}} \boldsymbol{{x}}\right)\boldsymbol{{tan}}^{\mathrm{2}} \boldsymbol{{x}}} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{−\mathrm{3}\left(\mathrm{2}\right)}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$$\left.\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\boldsymbol{{sin}}^{\mathrm{3}} \left(\boldsymbol{\pi}\mid\boldsymbol{{x}}\mid\right)}{{x}^{\mathrm{3}} }=\pm\boldsymbol{\pi} \\ $$$$\left.\mathrm{3}\right)\underset{{x}\rightarrow\boldsymbol{\mathrm{a}}} {\mathrm{lim}}\frac{\boldsymbol{\mathrm{lnx}}−\boldsymbol{\mathrm{lna}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{a}}_{} ^{\mathrm{2}} }=\underset{{x}\rightarrow\boldsymbol{\mathrm{a}}} {\mathrm{lim}}\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{a}}\right)}×\frac{\boldsymbol{\mathrm{lnx}}−\boldsymbol{\mathrm{lna}}}{\left(\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{a}}\right)} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{a}}}×\frac{\mathrm{1}}{\boldsymbol{\mathrm{a}}}=\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\left.\mathrm{4}\right)\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\pi{x}}\right).\boldsymbol{\mathrm{tan}}\left(\frac{\boldsymbol{\pi}}{\boldsymbol{{x}}}\right)=\mathrm{0}×\infty=\boldsymbol{\mathrm{FI}} \\ $$$$=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\boldsymbol{\mathrm{cos}}\left(\frac{\boldsymbol{\pi}}{\mathrm{2}}−\boldsymbol{\pi{x}}\right)\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi}}{\boldsymbol{\mathrm{x}}}\right) \\ $$$$\boldsymbol{\mathrm{posons}}\:\frac{\boldsymbol{\pi}}{\mathrm{2}}−\boldsymbol{{x}\pi}={X}=>\boldsymbol{{x}}=\frac{\boldsymbol{\pi}−\mathrm{2}\boldsymbol{{X}}}{\mathrm{2}\boldsymbol{\pi}} \\ $$$$\boldsymbol{{qd}}:\boldsymbol{{x}}\rightarrow\mathrm{2};\boldsymbol{{X}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$=\underset{\boldsymbol{{X}}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\mathrm{lim}}\boldsymbol{\mathrm{cosX}}.\boldsymbol{\mathrm{tan}}\left(\frac{\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} }{\boldsymbol{\pi}−\mathrm{2}\boldsymbol{{X}}}\right)=\mathrm{0}×\mathrm{0}=\mathrm{0} \\ $$$$ \\ $$$$\left.\:\mathrm{5}\right)\underset{{x}\rightarrow\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\mathrm{lim}}\left(\boldsymbol{{cos}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}−\boldsymbol{\mathrm{sin}}\frac{\boldsymbol{\mathrm{x}}}{\mathrm{2}}\right)\boldsymbol{\mathrm{tanx}}=\mathrm{0}×\infty=\boldsymbol{\mathrm{F}}\mathrm{I} \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$$\:\:\: \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *