Question Number 172762 by mnjuly1970 last updated on 01/Jul/22

Answered by aleks041103 last updated on 01/Jul/22

Commented by aleks041103 last updated on 01/Jul/22
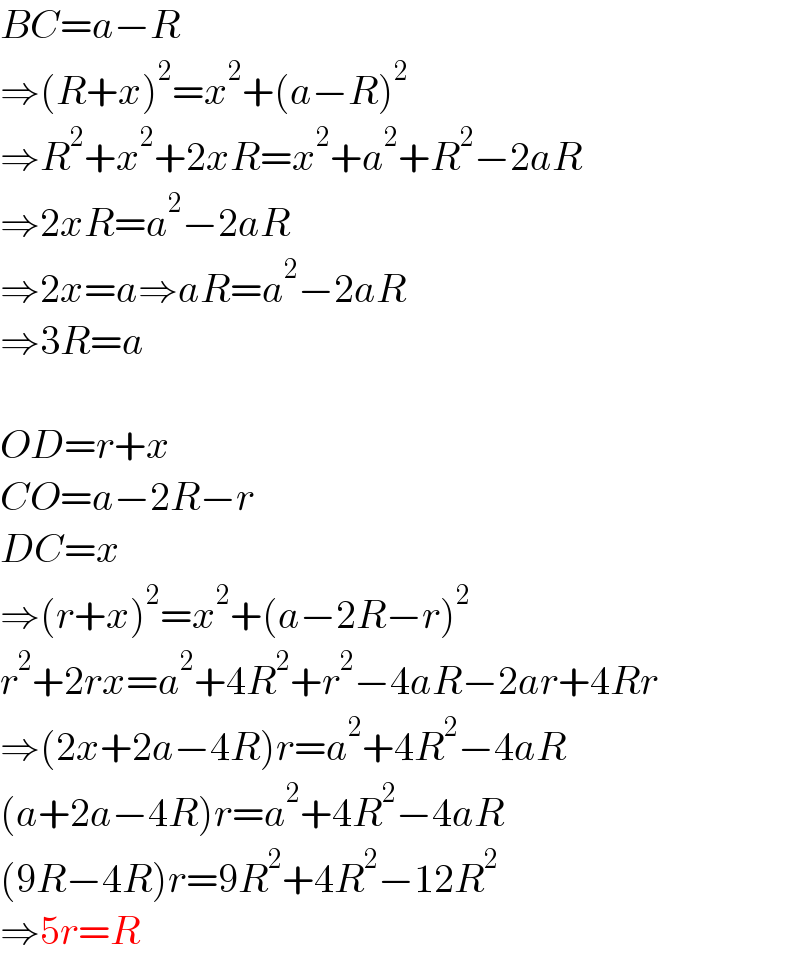
$${BC}={a}−{R} \\ $$$$\Rightarrow\left({R}+{x}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({a}−{R}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}^{\mathrm{2}} +{x}^{\mathrm{2}} +\mathrm{2}{xR}={x}^{\mathrm{2}} +{a}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{aR} \\ $$$$\Rightarrow\mathrm{2}{xR}={a}^{\mathrm{2}} −\mathrm{2}{aR} \\ $$$$\Rightarrow\mathrm{2}{x}={a}\Rightarrow{aR}={a}^{\mathrm{2}} −\mathrm{2}{aR} \\ $$$$\Rightarrow\mathrm{3}{R}={a} \\ $$$$ \\ $$$${OD}={r}+{x} \\ $$$${CO}={a}−\mathrm{2}{R}−{r} \\ $$$${DC}={x} \\ $$$$\Rightarrow\left({r}+{x}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\left({a}−\mathrm{2}{R}−{r}\right)^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} +\mathrm{2}{rx}={a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{4}{aR}−\mathrm{2}{ar}+\mathrm{4}{Rr} \\ $$$$\Rightarrow\left(\mathrm{2}{x}+\mathrm{2}{a}−\mathrm{4}{R}\right){r}={a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{aR} \\ $$$$\left({a}+\mathrm{2}{a}−\mathrm{4}{R}\right){r}={a}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} −\mathrm{4}{aR} \\ $$$$\left(\mathrm{9}{R}−\mathrm{4}{R}\right){r}=\mathrm{9}{R}^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} −\mathrm{12}{R}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{5}{r}={R} \\ $$
Commented by mnjuly1970 last updated on 01/Jul/22

$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 01/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
