Question Number 172785 by mnjuly1970 last updated on 01/Jul/22

Answered by Eulerian last updated on 01/Jul/22
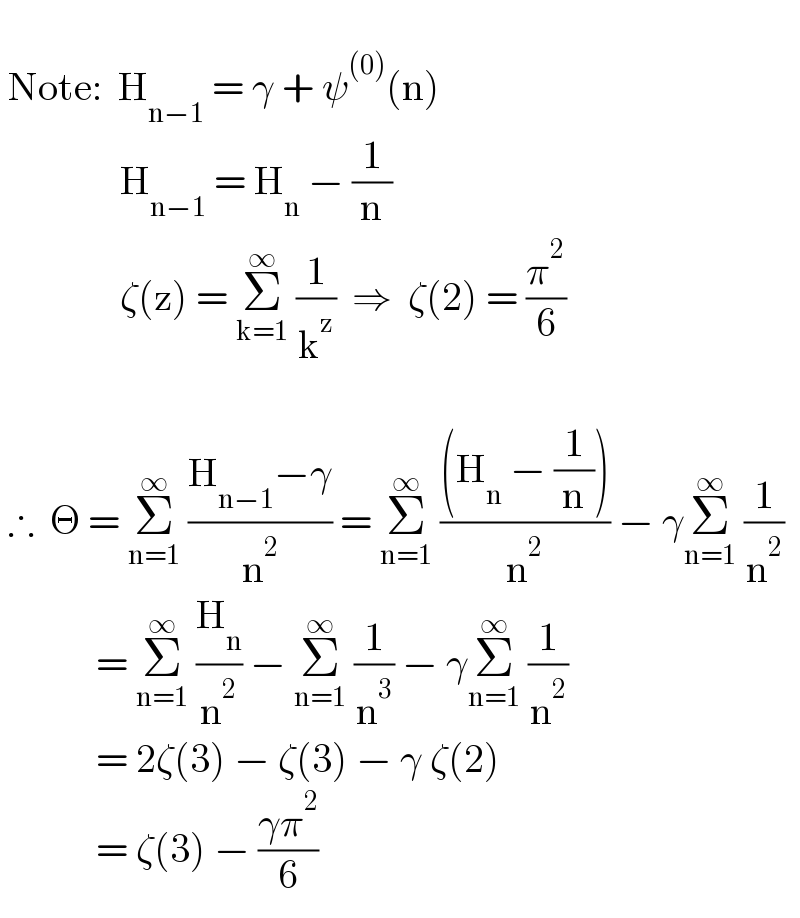
$$\: \\ $$$$\:\mathrm{Note}:\:\:\mathrm{H}_{\mathrm{n}−\mathrm{1}} \:=\:\gamma\:+\:\psi^{\left(\mathrm{0}\right)} \left(\mathrm{n}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{H}_{\mathrm{n}−\mathrm{1}} \:=\:\mathrm{H}_{\mathrm{n}} \:−\:\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\zeta\left(\mathrm{z}\right)\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{z}} }\:\:\Rightarrow\:\:\zeta\left(\mathrm{2}\right)\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\:\: \\ $$$$\:\therefore\:\:\Theta\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{H}_{\mathrm{n}−\mathrm{1}} −\gamma}{\mathrm{n}^{\mathrm{2}} }\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(\mathrm{H}_{\mathrm{n}} \:−\:\frac{\mathrm{1}}{\mathrm{n}}\right)}{\mathrm{n}^{\mathrm{2}} }\:−\:\gamma\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{H}_{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:−\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:−\:\gamma\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\zeta\left(\mathrm{3}\right)\:−\:\zeta\left(\mathrm{3}\right)\:−\:\gamma\:\zeta\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\zeta\left(\mathrm{3}\right)\:−\:\frac{\gamma\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by mnjuly1970 last updated on 01/Jul/22

$$\mathrm{thanks}\:\mathrm{alot} \\ $$
