Question Number 172818 by Mikenice last updated on 01/Jul/22
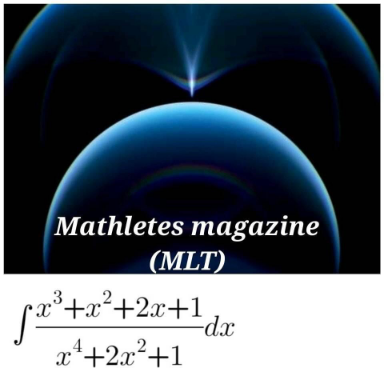
Answered by FelipeLz last updated on 02/Jul/22
![x^4 +2x^2 +1 = (x^2 +1)^2 I = ∫((x^3 +x^2 +2x+1)/(x^4 +2x^2 +1))dx = ∫(A/(x^2 +1))dx+∫(B/((x^2 +1)^2 ))dx A(x^2 +1)+B = x^3 +x^2 +2x+1 A(x^2 +1)+B = (x+1)x^2 +x+1+x A(x^2 +1)+B = (x+1)(x^2 +1)+x A = x+1 ∧ B = x I = ∫((x+1)/(x^2 +1))dx+∫(x/((x^2 +1)^2 ))dx = ∫(x/(x^2 +1))dx+∫(1/(x^2 +1))dx+∫(x/((x^2 +1)^2 ))dx I = (1/2)[ln(x^2 +1)−(1/(x^2 +1))]+tan^(−1) (x)+c](https://www.tinkutara.com/question/Q172831.png)
$${x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\:=\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$${I}\:=\:\int\frac{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:=\:\int\frac{{A}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\int\frac{{B}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:{A}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{B}\:=\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:{A}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{B}\:=\:\left({x}+\mathrm{1}\right){x}^{\mathrm{2}} +{x}+\mathrm{1}+{x} \\ $$$$\:\:\:\:\:\:{A}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{B}\:=\:\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{x} \\ $$$$\:\:\:\:\:\:{A}\:=\:{x}+\mathrm{1}\:\:\wedge\:\:{B}\:=\:{x} \\ $$$${I}\:=\:\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\:\int\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right]+\mathrm{tan}^{−\mathrm{1}} \left({x}\right)+{c} \\ $$
