Question Number 172819 by Mikenice last updated on 01/Jul/22

Answered by CElcedricjunior last updated on 02/Jul/22

$$\int\boldsymbol{\mathrm{x}}^{\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{\mathrm{arctan}}\left(\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{k}} \\ $$$$\left.\boldsymbol{\mathrm{posons}}\:\right)\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\mathrm{2}}} =\boldsymbol{\mathrm{a}}=>\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{ada}} \\ $$$$\boldsymbol{\mathrm{k}}=\int\boldsymbol{\mathrm{a}}^{\mathrm{4}} \boldsymbol{\mathrm{arctan}}\left(\boldsymbol{\mathrm{a}}\right)\boldsymbol{\mathrm{da}} \\ $$$$\:\:\boldsymbol{\mathrm{posons}}\:\begin{cases}{\boldsymbol{\mathrm{u}}=\boldsymbol{\mathrm{arctan}}\left(\boldsymbol{\mathrm{a}}\right)}\\{\boldsymbol{\mathrm{v}}'=\boldsymbol{{a}}^{\mathrm{4}} }\end{cases}=>\begin{cases}{\boldsymbol{\mathrm{u}}'=\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{v}}=\frac{\boldsymbol{\mathrm{a}}^{\mathrm{5}} }{\mathrm{5}}}\end{cases} \\ $$$$\boldsymbol{\mathrm{k}}=\frac{\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{arctana}}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\boldsymbol{\mathrm{a}}^{\mathrm{5}} +\boldsymbol{\mathrm{a}}^{\mathrm{3}} }{\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} }\boldsymbol{\mathrm{da}}+\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\boldsymbol{\mathrm{a}}^{\mathrm{3}} \boldsymbol{\mathrm{da}}}{\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{k}}=\boldsymbol{\mathrm{a}}\frac{\boldsymbol{\mathrm{arctana}}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{20}}\boldsymbol{\mathrm{a}}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\boldsymbol{\mathrm{a}}^{\mathrm{3}} +\boldsymbol{\mathrm{a}}}{\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} }\boldsymbol{\mathrm{da}}−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{da}}}{\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} } \\ $$$$\boldsymbol{\mathrm{k}}=\boldsymbol{\mathrm{a}}\frac{\boldsymbol{\mathrm{arctana}}}{\mathrm{5}}+\frac{\boldsymbol{\mathrm{a}}^{\mathrm{2}} }{\mathrm{10}}−\frac{\boldsymbol{\mathrm{a}}^{\mathrm{4}} }{\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{10}}\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)+\boldsymbol{\mathrm{cte}} \\ $$$$\int\boldsymbol{\mathrm{x}}^{\frac{\mathrm{3}}{\mathrm{2}}} \boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)=\boldsymbol{\mathrm{k}} \\ $$$$\boldsymbol{\mathrm{k}}=\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\boldsymbol{\mathrm{x}}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)+\frac{\boldsymbol{\mathrm{x}}}{\mathrm{10}}−\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{10}}\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{c}} \\ $$$$\boldsymbol{\mathrm{c}}\in\mathbb{R} \\ $$$$ \\ $$$$……..\mathscr{L}{e}\:{c}\acute {{e}l}\grave {{e}bre}\:{cedric}\:{junior}………. \\ $$
Answered by Mathspace last updated on 02/Jul/22
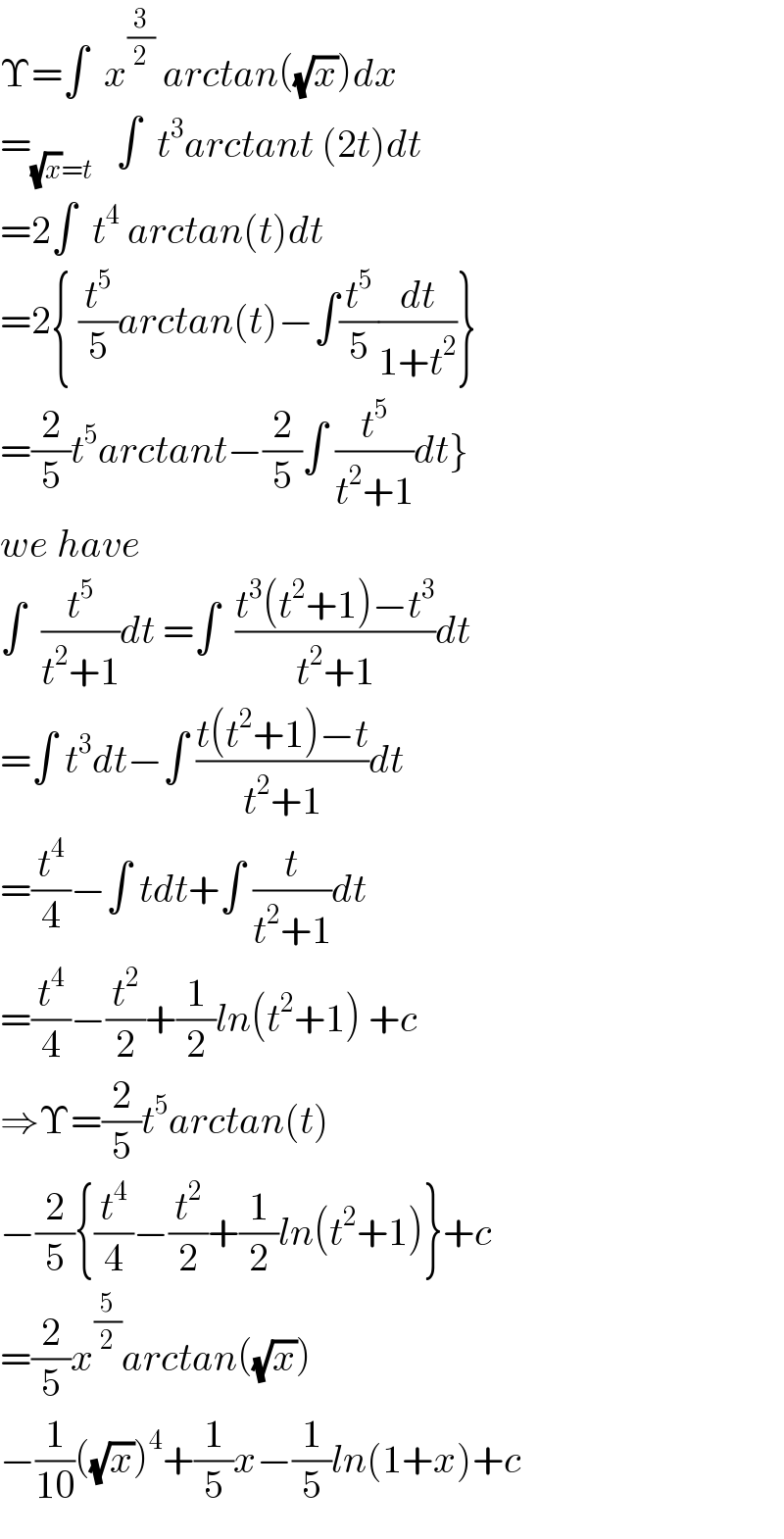
$$\Upsilon=\int\:\:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:{arctan}\left(\sqrt{{x}}\right){dx} \\ $$$$=_{\sqrt{{x}}={t}} \:\:\:\int\:\:{t}^{\mathrm{3}} {arctant}\:\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int\:\:{t}^{\mathrm{4}} \:{arctan}\left({t}\right){dt} \\ $$$$=\mathrm{2}\left\{\:\frac{{t}^{\mathrm{5}} }{\mathrm{5}}{arctan}\left({t}\right)−\int\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right\} \\ $$$$\left.=\frac{\mathrm{2}}{\mathrm{5}}{t}^{\mathrm{5}} {arctant}−\frac{\mathrm{2}}{\mathrm{5}}\int\:\frac{{t}^{\mathrm{5}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\right\} \\ $$$${we}\:{have} \\ $$$$\int\:\:\frac{{t}^{\mathrm{5}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:=\int\:\:\frac{{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)−{t}^{\mathrm{3}} }{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\int\:{t}^{\mathrm{3}} {dt}−\int\:\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)−{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\int\:{tdt}+\int\:\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+{c} \\ $$$$\Rightarrow\Upsilon=\frac{\mathrm{2}}{\mathrm{5}}{t}^{\mathrm{5}} {arctan}\left({t}\right) \\ $$$$−\frac{\mathrm{2}}{\mathrm{5}}\left\{\frac{{t}^{\mathrm{4}} }{\mathrm{4}}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\right\}+{c} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{5}}{\mathrm{2}}} {arctan}\left(\sqrt{{x}}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{10}}\left(\sqrt{{x}}\right)^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{5}}{x}−\frac{\mathrm{1}}{\mathrm{5}}{ln}\left(\mathrm{1}+{x}\right)+{c} \\ $$
Answered by thfchristopher last updated on 03/Jul/22
![∫x^(3/2) tan^(−1) (x^(1/2) )dx =(2/5)∫tan^(−1) (x^(1/2) )d(x^(5/2) ) =(2/5)x^(5/2) tan^(−1) (x^(1/2) )−(2/5)∫x^(5/2) [(1/(2(√x)(1+x)))]dx =(2/5)x^(5/2) tan^(−1) (x^(1/2) )−(1/5)∫(x^2 /(1+x))dx (1/5)∫(x^2 /(1+x))dx Let u=1+x du=dx ∴ (1/5)∫(x^2 /(1+x))dx =(1/5)∫(((u−1)^2 )/u)du =(1/5)∫(u−2+(1/u))du =(1/5)((u^2 /2)−2u+ln u)+C =(1/5)[(((1+x)^2 )/2)−2(1+x)+ln ∣1+x∣]+C Hence, ∫x^(3/2) tan^(−1) (x^(1/2) )dx =(2/5)x^(5/2) tan^(−1) (x^(1/2) )−(1/5)[(((1+x)^2 )/2)−2(1+x)+ln ∣1+x∣]+C](https://www.tinkutara.com/question/Q172898.png)
$$\int{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right){dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\int\mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right){d}\left({x}^{\frac{\mathrm{5}}{\mathrm{2}}} \right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)−\frac{\mathrm{2}}{\mathrm{5}}\int{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}\left(\mathrm{1}+{x}\right)}\right]{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)−\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}{dx} \\ $$$$\mathrm{Let}\:{u}=\mathrm{1}+{x} \\ $$$${du}={dx} \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\frac{\left({u}−\mathrm{1}\right)^{\mathrm{2}} }{{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int\left({u}−\mathrm{2}+\frac{\mathrm{1}}{{u}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{u}+\mathrm{ln}\:{u}\right)+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\left[\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\left(\mathrm{1}+{x}\right)+\mathrm{ln}\:\mid\mathrm{1}+{x}\mid\right]+{C} \\ $$$$\mathrm{Hence}, \\ $$$$\int{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right){dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{5}}{\mathrm{2}}} \mathrm{tan}^{−\mathrm{1}} \left({x}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)−\frac{\mathrm{1}}{\mathrm{5}}\left[\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\left(\mathrm{1}+{x}\right)+\mathrm{ln}\:\mid\mathrm{1}+{x}\mid\right]+{C} \\ $$
