Question Number 172862 by dragan91 last updated on 02/Jul/22
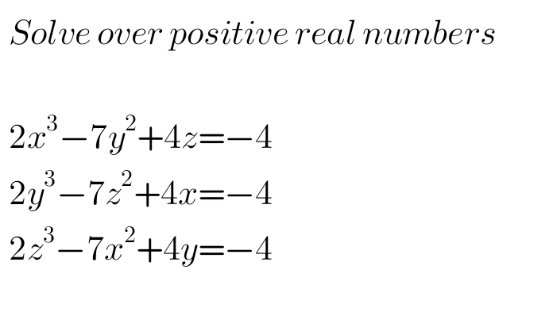
Commented by MJS_new last updated on 02/Jul/22
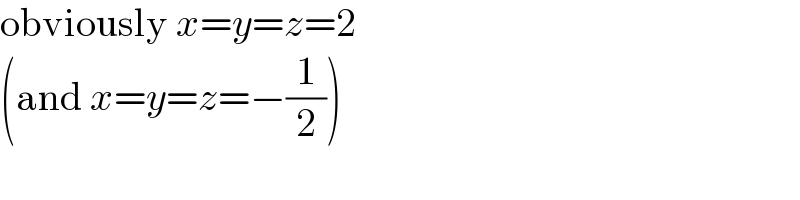
$$\mathrm{obviously}\:{x}={y}={z}=\mathrm{2} \\ $$$$\left(\mathrm{and}\:{x}={y}={z}=−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by Mikenice last updated on 02/Jul/22
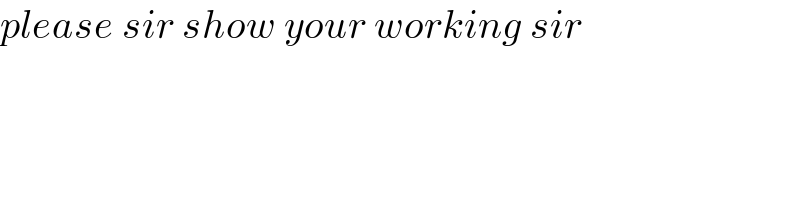
$${please}\:{sir}\:{show}\:{your}\:{working}\:{sir} \\ $$
Commented by MJS_new last updated on 02/Jul/22
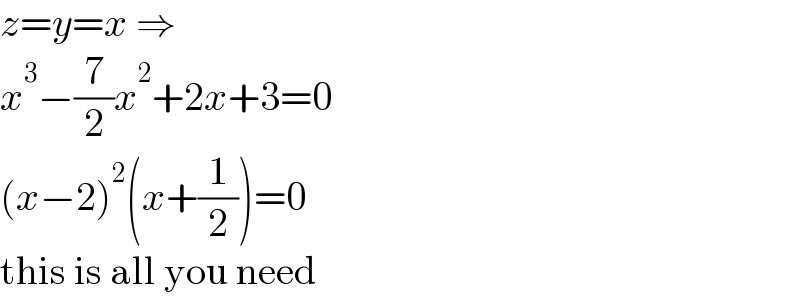
$${z}={y}={x}\:\Rightarrow \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} \left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{all}\:\mathrm{you}\:\mathrm{need} \\ $$
Commented by Mikenice last updated on 02/Jul/22
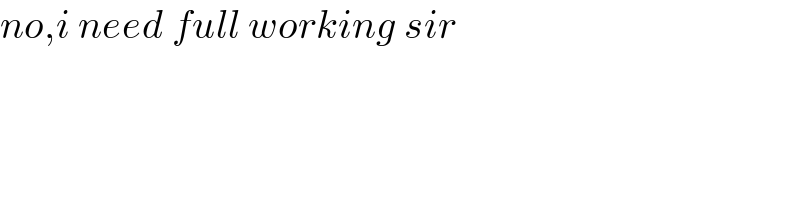
$${no},{i}\:{need}\:{full}\:{working}\:{sir} \\ $$
Commented by MJS_new last updated on 02/Jul/22
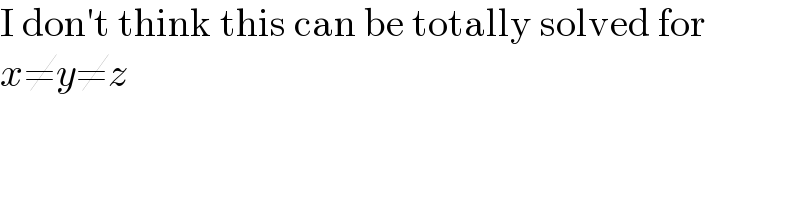
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{totally}\:\mathrm{solved}\:\mathrm{for} \\ $$$${x}\neq{y}\neq{z} \\ $$
