Question Number 172918 by mnjuly1970 last updated on 03/Jul/22

Commented by som(math1967) last updated on 03/Jul/22

$$\boldsymbol{{yes}}\:\boldsymbol{{i}}\:\boldsymbol{{got}}\:\frac{\mathrm{16}}{\mathrm{3}}\boldsymbol{{cm}} \\ $$
Commented by infinityaction last updated on 03/Jul/22

$$\frac{\mathrm{16}}{\mathrm{3}}\:??? \\ $$
Commented by som(math1967) last updated on 03/Jul/22

Commented by som(math1967) last updated on 03/Jul/22
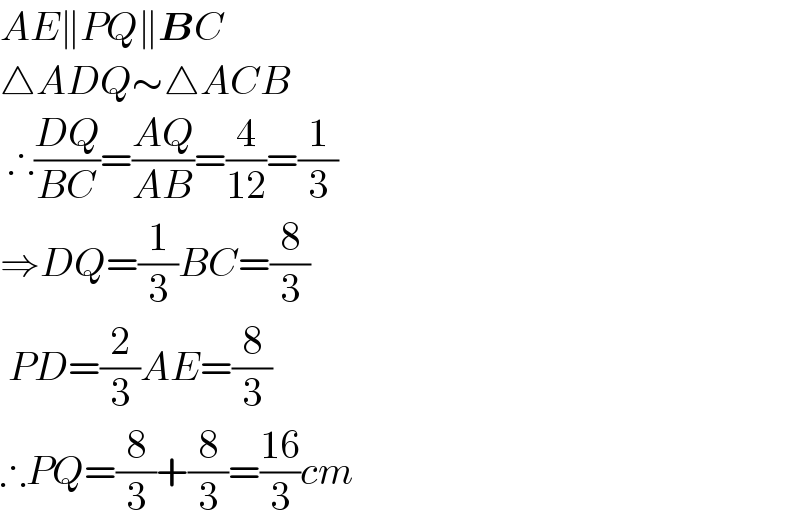
$${AE}\parallel{PQ}\parallel\boldsymbol{{B}}{C} \\ $$$$\bigtriangleup{ADQ}\sim\bigtriangleup{ACB} \\ $$$$\:\therefore\frac{{DQ}}{{BC}}=\frac{{AQ}}{{AB}}=\frac{\mathrm{4}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{DQ}=\frac{\mathrm{1}}{\mathrm{3}}{BC}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\:{PD}=\frac{\mathrm{2}}{\mathrm{3}}{AE}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$\therefore{PQ}=\frac{\mathrm{8}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{3}}=\frac{\mathrm{16}}{\mathrm{3}}{cm} \\ $$
Commented by mnjuly1970 last updated on 03/Jul/22

$$\mathrm{excellent}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 03/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by infinityaction last updated on 04/Jul/22

Commented by infinityaction last updated on 04/Jul/22
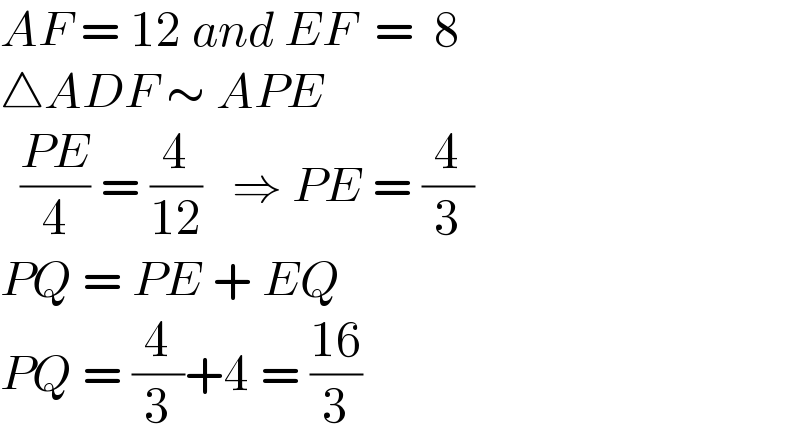
$${AF}\:=\:\mathrm{12}\:{and}\:{EF}\:\:=\:\:\mathrm{8} \\ $$$$\bigtriangleup{ADF}\:\sim\:{APE} \\ $$$$\:\:\frac{{PE}}{\mathrm{4}}\:=\:\frac{\mathrm{4}}{\mathrm{12}}\:\:\:\Rightarrow\:{PE}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${PQ}\:=\:{PE}\:+\:{EQ} \\ $$$${PQ}\:=\:\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{4}\:=\:\frac{\mathrm{16}}{\mathrm{3}} \\ $$
Commented by Tawa11 last updated on 06/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
