Question Number 173033 by cortano1 last updated on 05/Jul/22

Answered by greougoury555 last updated on 05/Jul/22
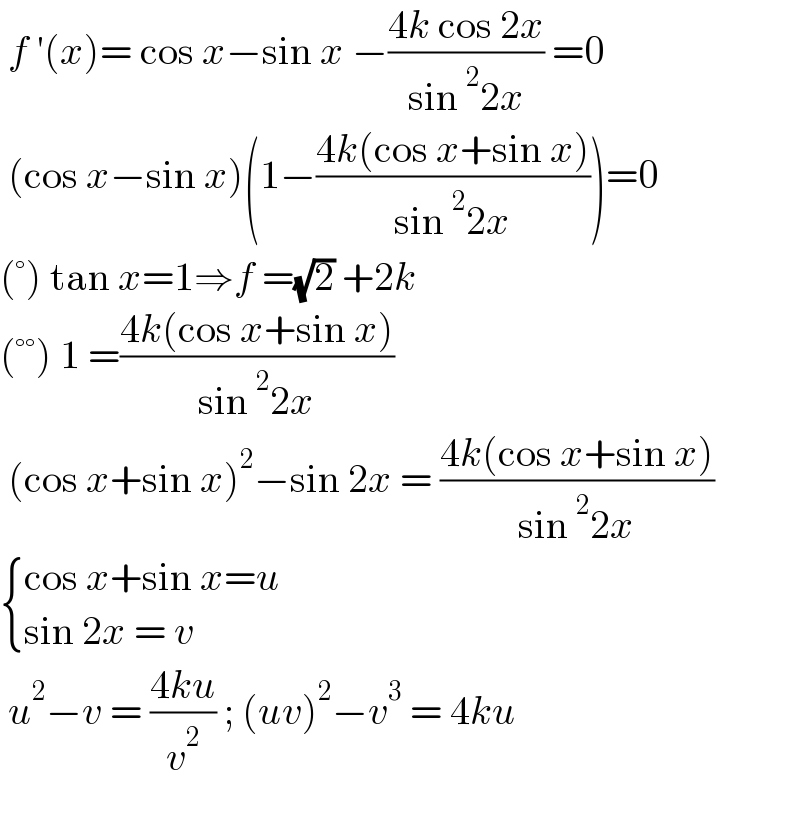
$$\:{f}\:'\left({x}\right)=\:\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\:−\frac{\mathrm{4}{k}\:\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\:=\mathrm{0} \\ $$$$\:\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left(\mathrm{1}−\frac{\mathrm{4}{k}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\right)=\mathrm{0} \\ $$$$\left(°\right)\:\mathrm{tan}\:{x}=\mathrm{1}\Rightarrow{f}\:=\sqrt{\mathrm{2}}\:+\mathrm{2}{k}\: \\ $$$$\left(°°\right)\:\mathrm{1}\:=\frac{\mathrm{4}{k}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$\:\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} −\mathrm{sin}\:\mathrm{2}{x}\:=\:\frac{\mathrm{4}{k}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$\begin{cases}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}={u}}\\{\mathrm{sin}\:\mathrm{2}{x}\:=\:{v}}\end{cases} \\ $$$$\:{u}^{\mathrm{2}} −{v}\:=\:\frac{\mathrm{4}{ku}}{{v}^{\mathrm{2}} }\:;\:\left({uv}\right)^{\mathrm{2}} −{v}^{\mathrm{3}} \:=\:\mathrm{4}{ku} \\ $$$$ \\ $$
Answered by a.lgnaoui last updated on 05/Jul/22
![f(x)=sin x+cos x+((2k)/(sin 2x)) limf(x)_(x→0) =1+(1/x)lim_(x→0) ((2x)/(sin 2x))k=1+(k/x) if k>0 f→+∞; if k<0 f→−∞ lim_(x→(π/2)) f(x)=1+lim_(x→(π/2)) ((2k)/(sin 2x))=+∞ if k>0 or −∞ if k<0 donc f decroissant et criissant si k>0 et contraire pour k>0 f′(x)=cos x−sin x−k((cos^2 x−sin^2 x)/(sin^2 xcos^2 x))=(cos x−sin x)[1−k((1/(cos x))+(1/(sin x)))] remarque x=(π/4) ⇒f′(x)=0 donc (π/4) is minimum of f(x).](https://www.tinkutara.com/question/Q173040.png)
$${f}\left({x}\right)=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\frac{\mathrm{2}{k}}{\mathrm{sin}\:\mathrm{2}{x}} \\ $$$${limf}\left({x}\right)_{{x}\rightarrow\mathrm{0}} =\mathrm{1}+\frac{\mathrm{1}}{{x}}{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{2}{x}}{\mathrm{sin}\:\mathrm{2}{x}}{k}=\mathrm{1}+\frac{{k}}{{x}} \\ $$$${if}\:{k}>\mathrm{0}\:\:\:\:\:\:{f}\rightarrow+\infty;\:\:\:\:{if}\:{k}<\mathrm{0}\:\:\:{f}\rightarrow−\infty \\ $$$${lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {f}\left({x}\right)=\mathrm{1}+{lim}_{{x}\rightarrow\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{k}}{\mathrm{sin}\:\mathrm{2}{x}}=+\infty\:\:\:{if}\:{k}>\mathrm{0}\:\:{or}\:−\infty\:\:{if}\:{k}<\mathrm{0} \\ $$$${donc}\:{f}\:{decroissant}\:{et}\:{criissant}\:\:{si}\:{k}>\mathrm{0}\:{et}\:{contraire}\:\:{pour}\:{k}>\mathrm{0} \\ $$$${f}'\left({x}\right)=\mathrm{cos}\:{x}−\mathrm{sin}\:{x}−{k}\frac{\mathrm{cos}\:^{\mathrm{2}} {x}−\mathrm{sin}\:^{\mathrm{2}} {x}}{\mathrm{sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}}=\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)\left[\mathrm{1}−{k}\left(\frac{\mathrm{1}}{\mathrm{cos}\:{x}}+\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\right)\right] \\ $$$${remarque}\:{x}=\frac{\pi}{\mathrm{4}}\:\Rightarrow{f}'\left({x}\right)=\mathrm{0}\:\:\:{donc}\:\frac{\pi}{\mathrm{4}}\:{is}\:{minimum}\:{of}\:{f}\left({x}\right). \\ $$
