Question Number 173049 by Shrinava last updated on 05/Jul/22

Answered by MJS_new last updated on 06/Jul/22
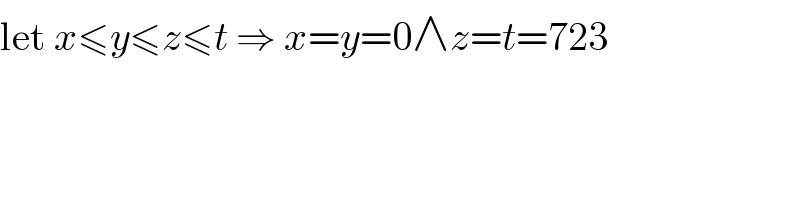
$$\mathrm{let}\:{x}\leqslant{y}\leqslant{z}\leqslant{t}\:\Rightarrow\:{x}={y}=\mathrm{0}\wedge{z}={t}=\mathrm{723} \\ $$
Answered by dragan91 last updated on 06/Jul/22

$${Let}\:{x}\leqslant{y}\leqslant{z}\leqslant{t}\:{and} \\ $$$${x}={y}\:{and}\:{z}={t} \\ $$$$\mathrm{2}{x}+\mathrm{2}{z}=\mathrm{1446} \\ $$$$\:{x}+{z}=\mathrm{723} \\ $$$${x}!{x}!{z}!={z}! \\ $$$$\left({x}!\right)^{\mathrm{2}} =\mathrm{1}\Rightarrow\:{x}={y}=\mathrm{1} \\ $$$${then}\:{t}={z}=\mathrm{722} \\ $$$$\underline{\left({x},{y},{z},{t}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{722},\mathrm{722}\right)} \\ $$$${for}\:{x}\neq{y}\neq{z}\neq{t}\:{and}\:{x}=\mathrm{1} \\ $$$${Notice}\:\mathrm{6}!=\mathrm{720}\:{let}\:\:{y}=\mathrm{6} \\ $$$$\mathrm{1}!\mathrm{6}!{z}!={t}! \\ $$$$\mathrm{720}\centerdot\mathrm{719}!=\mathrm{720}!\Rightarrow{z}=\mathrm{719},{t}=\mathrm{720} \\ $$$${check} \\ $$$$\mathrm{1}+\mathrm{6}+\mathrm{719}+\mathrm{720}=\mathrm{1446}\checkmark \\ $$$$\mathrm{1}!\mathrm{6}!\mathrm{719}!=\mathrm{720}! \\ $$$$\left({x},{y},{z},{t}\right)=\left(\mathrm{1},\mathrm{6},\mathrm{719},\mathrm{720}\right) \\ $$$${ALL}\:{SOLUTIONS} \\ $$$$\left({x},{y},{z},{t}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{722},\mathrm{722}\right) \\ $$$$\left({x},{y},{z},{t}\right)=\left(\mathrm{1},\mathrm{6},\mathrm{719},\mathrm{720}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by MJS_new last updated on 06/Jul/22
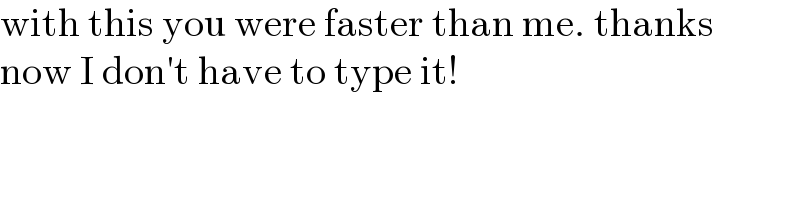
$$\mathrm{with}\:\mathrm{this}\:\mathrm{you}\:\mathrm{were}\:\mathrm{faster}\:\mathrm{than}\:\mathrm{me}.\:\mathrm{thanks} \\ $$$$\mathrm{now}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{to}\:\mathrm{type}\:\mathrm{it}! \\ $$
Commented by dragan91 last updated on 06/Jul/22

$$\mathrm{Yes}.\mathrm{U}\:\mathrm{are}\:\mathrm{right}.\:\mathrm{Thanks} \\ $$
