Question Number 173065 by mnjuly1970 last updated on 06/Jul/22
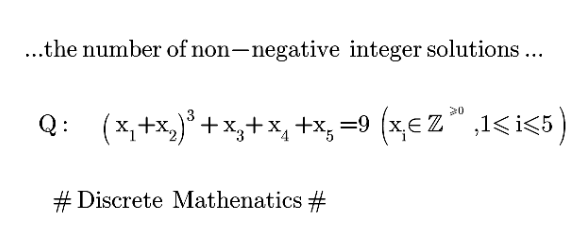
Commented by a.lgnaoui last updated on 06/Jul/22

$$\mathrm{103} \\ $$
Commented by mr W last updated on 06/Jul/22

$$\mathrm{154}\:{solutions}\:? \\ $$
Commented by mnjuly1970 last updated on 06/Jul/22
$$\mathrm{yes}\:\:\mathrm{sir}\:\:\mathrm{W}\:\mathrm{thanks}\:\mathrm{alot}… \\ $$$$\mathrm{grateful}\:…. \\ $$
Answered by mr W last updated on 06/Jul/22

$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{3}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +{x}_{\mathrm{5}} =\mathrm{9}\:{with}\:{x}_{{i}} \geqslant\mathrm{0}. \\ $$$${say}\:{A}=\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$${say}\:{B}={x}_{\mathrm{3}} +{x}_{\mathrm{4}} +{x}_{\mathrm{5}} \\ $$$${A}+{B}=\mathrm{9} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:{A}=\mathrm{0},\:{B}=\mathrm{9} \\ $$$${A}=\mathrm{0}\:\Rightarrow{x}_{\mathrm{1}} ={x}_{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{1}\:{possibility} \\ $$$${B}=\mathrm{9}: \\ $$$$\left(\mathrm{1}+{t}+{t}^{\mathrm{2}} +…\right)^{\mathrm{3}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {t}^{{k}} \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{9}+\mathrm{2}} =\mathrm{55}\:{solutions} \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{A}=\mathrm{1},\:{B}=\mathrm{8} \\ $$$${A}=\mathrm{1}\: \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\mathrm{0},\:{x}_{\mathrm{2}} =\mathrm{1}\:{or}\:{x}_{\mathrm{1}} =\mathrm{1},\:{x}_{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{2}\:{possibilities} \\ $$$${B}=\mathrm{8}: \\ $$$$\Rightarrow{C}_{\mathrm{2}} ^{\mathrm{8}+\mathrm{2}} =\mathrm{45}\:{possibilities} \\ $$$$\Rightarrow\mathrm{2}×\mathrm{45}=\mathrm{90}\:{solutions} \\ $$$$ \\ $$$${case}\:\mathrm{3}:\:{A}=\mathrm{8},\:{B}=\mathrm{1} \\ $$$${A}=\mathrm{8}\: \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\mathrm{0},\:{x}_{\mathrm{2}} =\mathrm{2}\:{or}\:{x}_{\mathrm{1}} ={x}_{\mathrm{2}} =\mathrm{1}\:{or}\:{x}_{\mathrm{1}} =\mathrm{2},\:{x}_{\mathrm{2}} =\mathrm{0}\:\Rightarrow\mathrm{3}\:{possibilities} \\ $$$${B}=\mathrm{1}\:\Rightarrow\mathrm{3}\:{possibilities} \\ $$$$\Rightarrow\mathrm{3}×\mathrm{3}=\mathrm{9}\:{solutions} \\ $$$$ \\ $$$${totally}:\: \\ $$$$\mathrm{55}+\mathrm{90}+\mathrm{9}=\mathrm{154}\:{solutions}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 06/Jul/22
$$\:\:\:\:\:\mathrm{excellent}\:\:\mathrm{as}\:\mathrm{always}\:\mathrm{sir}\:\mathrm{W}.. \\ $$
Commented by mr W last updated on 06/Jul/22

$${thanks}\:{sir}! \\ $$
Commented by Tawa11 last updated on 06/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
