Question Number 173124 by peter frank last updated on 06/Jul/22
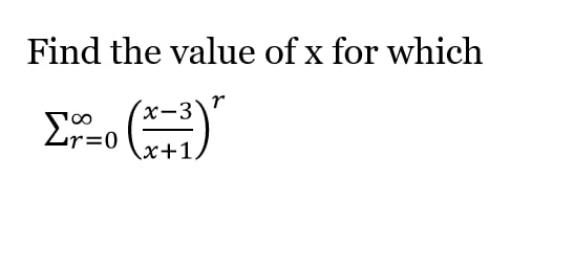
Commented by aleks041103 last updated on 06/Jul/22
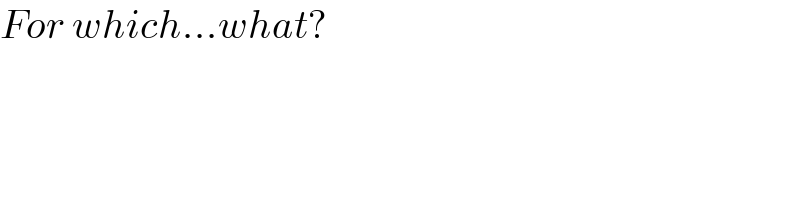
$${For}\:{which}…{what}? \\ $$
Commented by peter frank last updated on 07/Jul/22
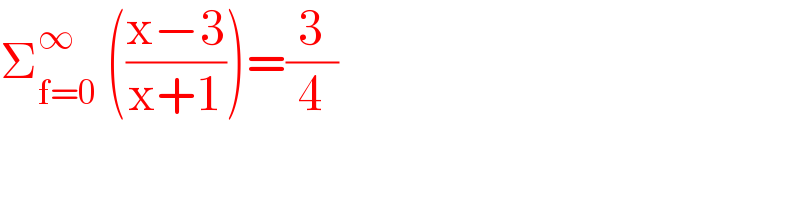
$$\sum_{\mathrm{f}=\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{x}+\mathrm{1}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Answered by Mathspace last updated on 06/Jul/22
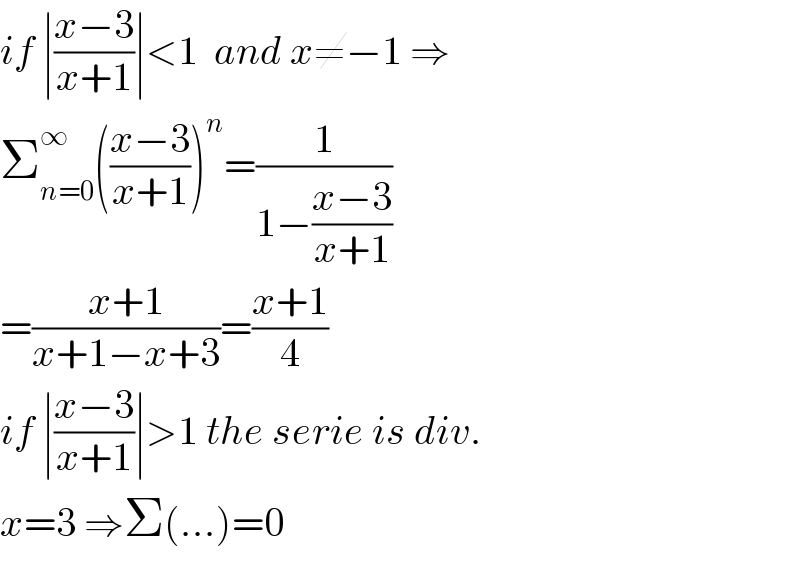
$${if}\:\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}}\mid<\mathrm{1}\:\:{and}\:{x}\neq−\mathrm{1}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \left(\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}}\right)^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}}} \\ $$$$=\frac{{x}+\mathrm{1}}{{x}+\mathrm{1}−{x}+\mathrm{3}}=\frac{{x}+\mathrm{1}}{\mathrm{4}} \\ $$$${if}\:\mid\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}}\mid>\mathrm{1}\:{the}\:{serie}\:{is}\:{div}. \\ $$$${x}=\mathrm{3}\:\Rightarrow\Sigma\left(…\right)=\mathrm{0} \\ $$
Answered by aleks041103 last updated on 07/Jul/22

$${let}\:{a}=\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}{a}^{{r}} =\frac{\mathrm{1}}{\mathrm{1}−{a}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{1}−{a}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${a}=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{3}}={a} \\ $$$${since}\:\mid{a}\mid<\mathrm{1},\:{the}\:{sum}\:{really}\:{converges} \\ $$$$\frac{{x}−\mathrm{3}}{{x}+\mathrm{1}}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}\left({x}−\mathrm{3}\right)=−\left({x}+\mathrm{1}\right) \\ $$$$\mathrm{3}{x}−\mathrm{9}=−{x}−\mathrm{1} \\ $$$$\mathrm{4}{x}−\mathrm{9}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{4}{x}−\mathrm{8}=\mathrm{0} \\ $$$${x}−\mathrm{2}=\mathrm{0} \\ $$$${x}=\mathrm{2} \\ $$
