Question-173139

Question Number 173139 by mnjuly1970 last updated on 07/Jul/22

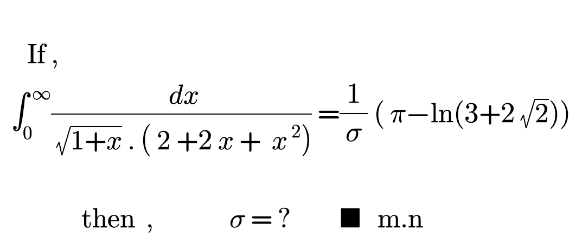
Answered by Mathspace last updated on 07/Jul/22

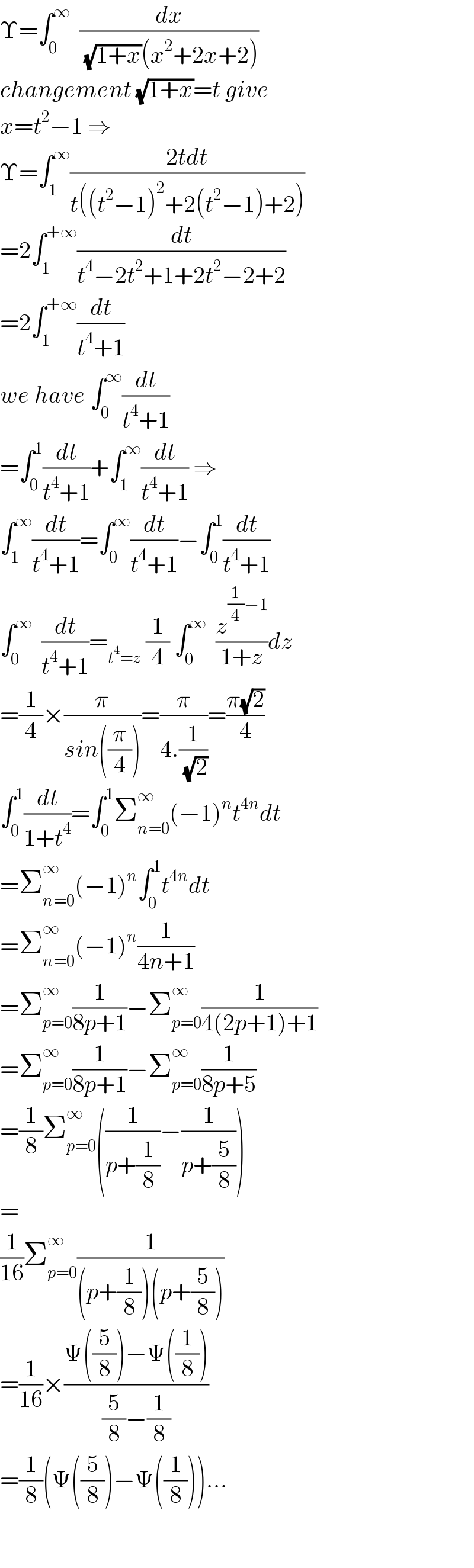
Υ=∫_0 ^∞ (dx/( (√(1+x))(x^2 +2x+2))) changement (√(1+x))=t give x=t^2 −1 ⇒ Υ=∫_1 ^∞ ((2tdt)/(t((t^2 −1)^2 +2(t^2 −1)+2))) =2∫_1 ^(+∞) (dt/(t^4 −2t^2 +1+2t^2 −2+2)) =2∫_1 ^(+∞) (dt/(t^4 +1)) we have ∫_0 ^∞ (dt/(t^4 +1)) =∫_0 ^1 (dt/(t^4 +1))+∫_1 ^∞ (dt/(t^4 +1)) ⇒ ∫_1 ^∞ (dt/(t^4 +1))=∫_0 ^∞ (dt/(t^4 +1))−∫_0 ^1 (dt/(t^4 +1)) ∫_0 ^∞ (dt/(t^4 +1))=_(t^4 =z) (1/4) ∫_0 ^∞ (z^((1/4)−1) /(1+z))dz =(1/4)×(π/(sin((π/4))))=(π/(4.(1/( (√2)))))=((π(√2))/4) ∫_0 ^1 (dt/(1+t^4 ))=∫_0 ^1 Σ_(n=0) ^∞ (−1)^n t^(4n) dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 t^(4n) dt =Σ_(n=0) ^∞ (−1)^n (1/(4n+1)) =Σ_(p=0) ^∞ (1/(8p+1))−Σ_(p=0) ^∞ (1/(4(2p+1)+1)) =Σ_(p=0) ^∞ (1/(8p+1))−Σ_(p=0) ^∞ (1/(8p+5)) =(1/8)Σ_(p=0) ^∞ ((1/(p+(1/8)))−(1/(p+(5/8)))) = (1/(16))Σ_(p=0) ^∞ (1/((p+(1/8))(p+(5/8)))) =(1/(16))×((Ψ((5/8))−Ψ((1/8)))/((5/8)−(1/8))) =(1/8)(Ψ((5/8))−Ψ((1/8)))...

$$\Upsilon=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{2}\right)} \\ $$$${changement}\:\sqrt{\mathrm{1}+{x}}={t}\:{give} \\ $$$${x}={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow \\ $$$$\Upsilon=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{2}{tdt}}{{t}\left(\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left({t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{2}\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{+\infty} \frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}+\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{+\infty} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}+\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}=\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{{t}^{\mathrm{4}} +\mathrm{1}}=_{{t}^{\mathrm{4}} ={z}} \:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{z}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{z}}{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}=\frac{\pi}{\mathrm{4}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {t}^{\mathrm{4}{n}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{4}{n}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{1}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{8}{p}+\mathrm{1}}−\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{p}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{8}{p}+\mathrm{1}}−\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{8}{p}+\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\sum_{{p}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{p}+\frac{\mathrm{1}}{\mathrm{8}}}−\frac{\mathrm{1}}{{p}+\frac{\mathrm{5}}{\mathrm{8}}}\right) \\ $$$$= \\ $$$$\frac{\mathrm{1}}{\mathrm{16}}\sum_{{p}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({p}+\frac{\mathrm{1}}{\mathrm{8}}\right)\left({p}+\frac{\mathrm{5}}{\mathrm{8}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}×\frac{\Psi\left(\frac{\mathrm{5}}{\mathrm{8}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{8}}\right)}{\frac{\mathrm{5}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\Psi\left(\frac{\mathrm{5}}{\mathrm{8}}\right)−\Psi\left(\frac{\mathrm{1}}{\mathrm{8}}\right)\right)… \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 07/Jul/22

$$\mathrm{bravo}\:\mathrm{sir}… \\ $$

Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply