Question Number 173164 by SANOGO last updated on 07/Jul/22
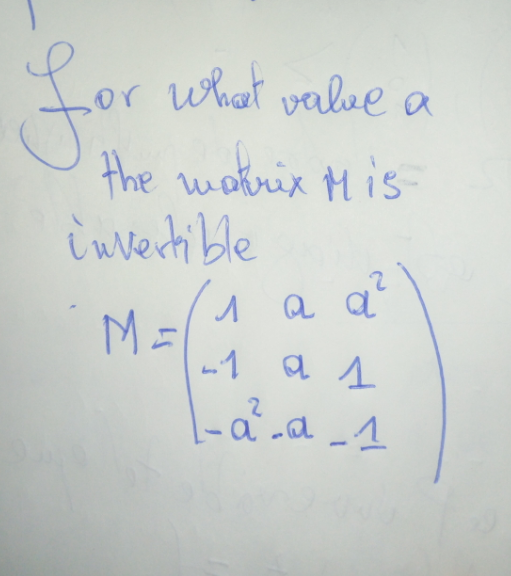
Answered by CElcedricjunior last updated on 08/Jul/22

$$\boldsymbol{\mathrm{det}}\left(\boldsymbol{\mathrm{M}}\right)=\mathrm{0}−\boldsymbol{\mathrm{a}}\left(\mathrm{1}+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right)+\boldsymbol{\mathrm{a}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{a}}+\boldsymbol{\mathrm{a}}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\mathrm{a}}\left(\boldsymbol{\mathrm{a}}^{\mathrm{4}} −\mathrm{1}\right) \\ $$$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{M}}\:\boldsymbol{\mathrm{inversible}}\:\boldsymbol{\mathrm{if}} \\ $$$$\boldsymbol{\mathrm{det}}\left(\boldsymbol{\mathrm{M}}\right)#\mathrm{0}=>\boldsymbol{\mathrm{a}}#\mathrm{0}\:\boldsymbol{\mathrm{et}}\:\boldsymbol{\mathrm{a}}#\mathrm{1} \\ $$$$\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{a}}\in\mathbb{R}\backslash\left\{\mathrm{0};\mathrm{1}\right\}\:\boldsymbol{\mathrm{Matrix}}\:\boldsymbol{\mathrm{M}}\:\boldsymbol{\mathrm{it}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{inversible}} \\ $$$$ \\ $$$$ \\ $$$$……{the}\:{celebre}\:{cedric}\:{junior}……. \\ $$
