Question Number 173188 by dragan91 last updated on 08/Jul/22

Answered by mr W last updated on 08/Jul/22
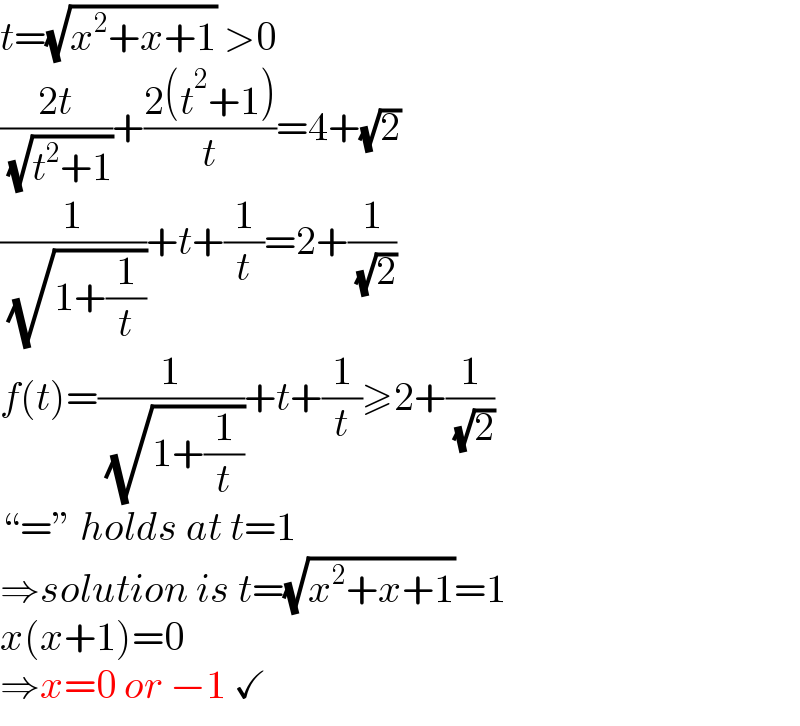
$${t}=\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:>\mathrm{0} \\ $$$$\frac{\mathrm{2}{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}+\frac{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{{t}}=\mathrm{4}+\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}}}}+{t}+\frac{\mathrm{1}}{{t}}=\mathrm{2}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{t}}}}+{t}+\frac{\mathrm{1}}{{t}}\geqslant\mathrm{2}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$“=''\:{holds}\:{at}\:{t}=\mathrm{1} \\ $$$$\Rightarrow{solution}\:{is}\:{t}=\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}=\mathrm{1} \\ $$$${x}\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0}\:{or}\:−\mathrm{1}\:\checkmark \\ $$
Commented by dragan91 last updated on 08/Jul/22

$$\mathrm{nice} \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
