Question Number 173212 by peter frank last updated on 08/Jul/22

Answered by Frix last updated on 08/Jul/22
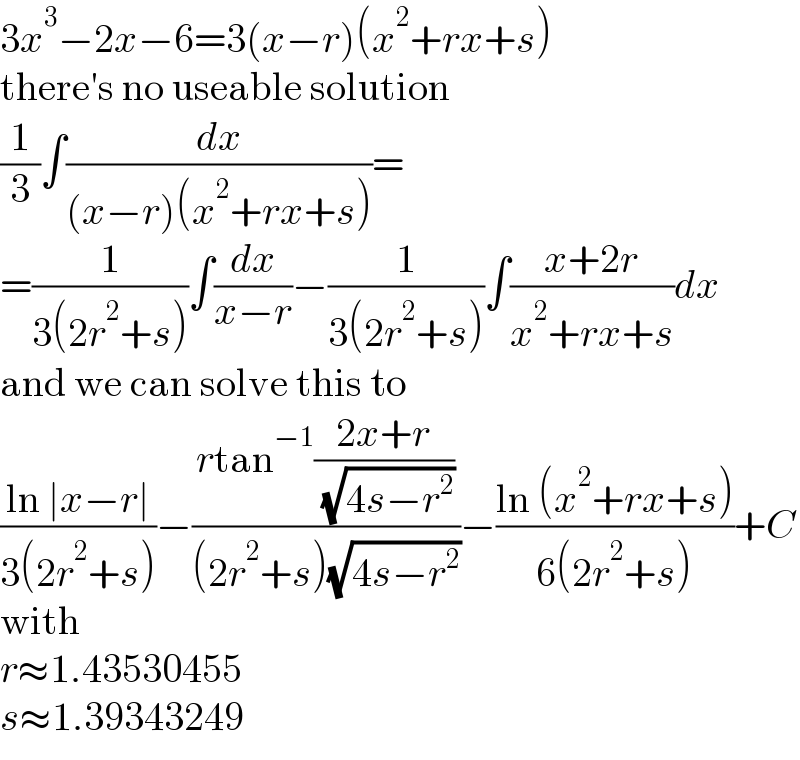
$$\mathrm{3}{x}^{\mathrm{3}} −\mathrm{2}{x}−\mathrm{6}=\mathrm{3}\left({x}−{r}\right)\left({x}^{\mathrm{2}} +{rx}+{s}\right) \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{useable}\:\mathrm{solution} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\left({x}−{r}\right)\left({x}^{\mathrm{2}} +{rx}+{s}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}{r}^{\mathrm{2}} +{s}\right)}\int\frac{{dx}}{{x}−{r}}−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{2}{r}^{\mathrm{2}} +{s}\right)}\int\frac{{x}+\mathrm{2}{r}}{{x}^{\mathrm{2}} +{rx}+{s}}{dx} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{to} \\ $$$$\frac{\mathrm{ln}\:\mid{x}−{r}\mid}{\mathrm{3}\left(\mathrm{2}{r}^{\mathrm{2}} +{s}\right)}−\frac{{r}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}+{r}}{\:\sqrt{\mathrm{4}{s}−{r}^{\mathrm{2}} }}}{\left(\mathrm{2}{r}^{\mathrm{2}} +{s}\right)\sqrt{\mathrm{4}{s}−{r}^{\mathrm{2}} }}−\frac{\mathrm{ln}\:\left({x}^{\mathrm{2}} +{rx}+{s}\right)}{\mathrm{6}\left(\mathrm{2}{r}^{\mathrm{2}} +{s}\right)}+{C} \\ $$$$\mathrm{with} \\ $$$${r}\approx\mathrm{1}.\mathrm{43530455} \\ $$$${s}\approx\mathrm{1}.\mathrm{39343249} \\ $$
Commented by Frix last updated on 08/Jul/22

$$\mathrm{yes}\:\mathrm{but}\:\mathrm{this}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{make}\:\mathrm{it}\:\mathrm{better}\:\mathrm{to}\:\mathrm{use}… \\ $$
Commented by mr W last updated on 08/Jul/22
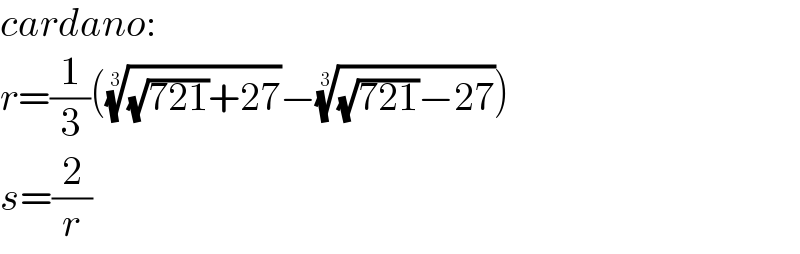
$${cardano}: \\ $$$${r}=\frac{\mathrm{1}}{\mathrm{3}}\left(\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{721}}+\mathrm{27}}−\sqrt[{\mathrm{3}}]{\sqrt{\mathrm{721}}−\mathrm{27}}\right) \\ $$$${s}=\frac{\mathrm{2}}{{r}} \\ $$
Commented by mr W last updated on 08/Jul/22

$${true}\:{sir}! \\ $$$${i}\:{just}\:{wanted}\:{to}\:{say}\:{that}\:{we}\:{can}\:{also} \\ $$$${get}\:{the}\:{exact}\:{values}\:{of}\:{r}\:{and}\:{s}. \\ $$
Commented by Frix last updated on 09/Jul/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
