Question-173227

Question Number 173227 by mnjuly1970 last updated on 08/Jul/22

Commented by mr W last updated on 08/Jul/22

$${not}\:\mathrm{1234567900}? \\ $$

Answered by floor(10²Eta[1]) last updated on 09/Jul/22

11=((10^2 −1)/9) 111=((10^3 −1)/9) let the wanted sum be equal to S ⇒S=((10^(10) −1)/9)+((10^9 −1)/9)+...+((10−1)/9) =(((10^(10) +10^9 +...+10)−10)/9) =((((10(10^(10) −1))/9)−10)/9)=((10^(11) −100)/(81))=((10^2 (10^9 −1))/(81)) =((100(999999999))/(81))=((11111111100)/9)

$$\mathrm{11}=\frac{\mathrm{10}^{\mathrm{2}} −\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{111}=\frac{\mathrm{10}^{\mathrm{3}} −\mathrm{1}}{\mathrm{9}} \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{wanted}\:\mathrm{sum}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{S} \\ $$$$\Rightarrow\mathrm{S}=\frac{\mathrm{10}^{\mathrm{10}} −\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{10}^{\mathrm{9}} −\mathrm{1}}{\mathrm{9}}+…+\frac{\mathrm{10}−\mathrm{1}}{\mathrm{9}} \\ $$$$=\frac{\left(\mathrm{10}^{\mathrm{10}} +\mathrm{10}^{\mathrm{9}} +…+\mathrm{10}\right)−\mathrm{10}}{\mathrm{9}} \\ $$$$=\frac{\frac{\mathrm{10}\left(\mathrm{10}^{\mathrm{10}} −\mathrm{1}\right)}{\mathrm{9}}−\mathrm{10}}{\mathrm{9}}=\frac{\mathrm{10}^{\mathrm{11}} −\mathrm{100}}{\mathrm{81}}=\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{10}^{\mathrm{9}} −\mathrm{1}\right)}{\mathrm{81}} \\ $$$$=\frac{\mathrm{100}\left(\mathrm{999999999}\right)}{\mathrm{81}}=\frac{\mathrm{11111111100}}{\mathrm{9}} \\ $$$$ \\ $$

Commented by peter frank last updated on 09/Jul/22

$$\mathrm{thank}\:\mathrm{you} \\ $$

Commented by MJS_new last updated on 09/Jul/22

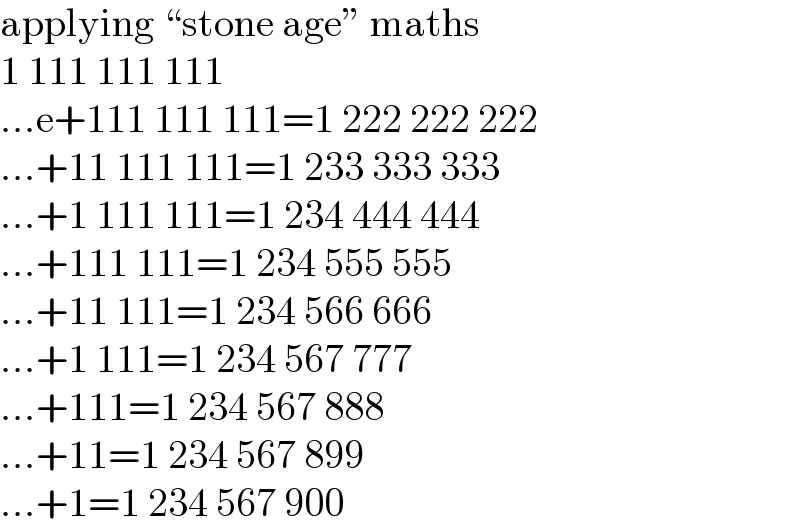
applying “stone age” maths 1 111 111 111 ...e+111 111 111=1 222 222 222 ...+11 111 111=1 233 333 333 ...+1 111 111=1 234 444 444 ...+111 111=1 234 555 555 ...+11 111=1 234 566 666 ...+1 111=1 234 567 777 ...+111=1 234 567 888 ...+11=1 234 567 899 ...+1=1 234 567 900

$$\mathrm{applying}\:“\mathrm{stone}\:\mathrm{age}''\:\mathrm{maths} \\ $$$$\mathrm{1}\:\mathrm{111}\:\mathrm{111}\:\mathrm{111} \\ $$$$…\mathrm{e}+\mathrm{111}\:\mathrm{111}\:\mathrm{111}=\mathrm{1}\:\mathrm{222}\:\mathrm{222}\:\mathrm{222} \\ $$$$…+\mathrm{11}\:\mathrm{111}\:\mathrm{111}=\mathrm{1}\:\mathrm{233}\:\mathrm{333}\:\mathrm{333} \\ $$$$…+\mathrm{1}\:\mathrm{111}\:\mathrm{111}=\mathrm{1}\:\mathrm{234}\:\mathrm{444}\:\mathrm{444} \\ $$$$…+\mathrm{111}\:\mathrm{111}=\mathrm{1}\:\mathrm{234}\:\mathrm{555}\:\mathrm{555} \\ $$$$…+\mathrm{11}\:\mathrm{111}=\mathrm{1}\:\mathrm{234}\:\mathrm{566}\:\mathrm{666} \\ $$$$…+\mathrm{1}\:\mathrm{111}=\mathrm{1}\:\mathrm{234}\:\mathrm{567}\:\mathrm{777} \\ $$$$…+\mathrm{111}=\mathrm{1}\:\mathrm{234}\:\mathrm{567}\:\mathrm{888} \\ $$$$…+\mathrm{11}=\mathrm{1}\:\mathrm{234}\:\mathrm{567}\:\mathrm{899} \\ $$$$…+\mathrm{1}=\mathrm{1}\:\mathrm{234}\:\mathrm{567}\:\mathrm{900} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply