Question Number 173273 by mr W last updated on 09/Jul/22

Commented by mr W last updated on 09/Jul/22
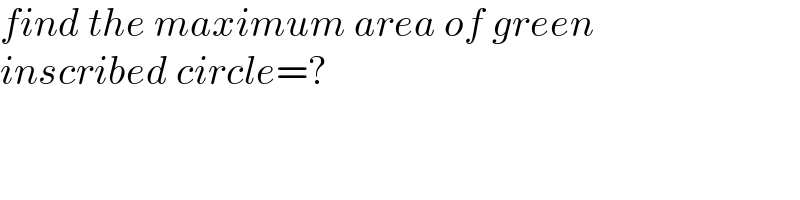
$${find}\:{the}\:{maximum}\:{area}\:{of}\:{green} \\ $$$${inscribed}\:{circle}=? \\ $$
Answered by mr W last updated on 09/Jul/22
Commented by mr W last updated on 09/Jul/22
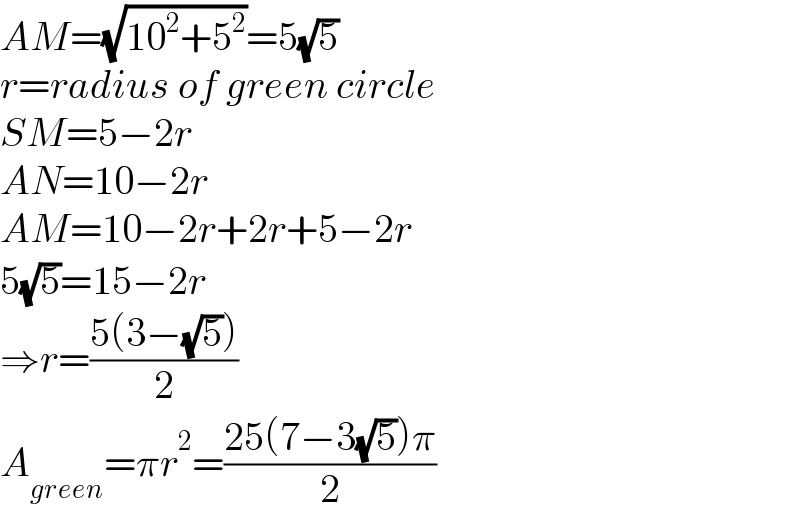
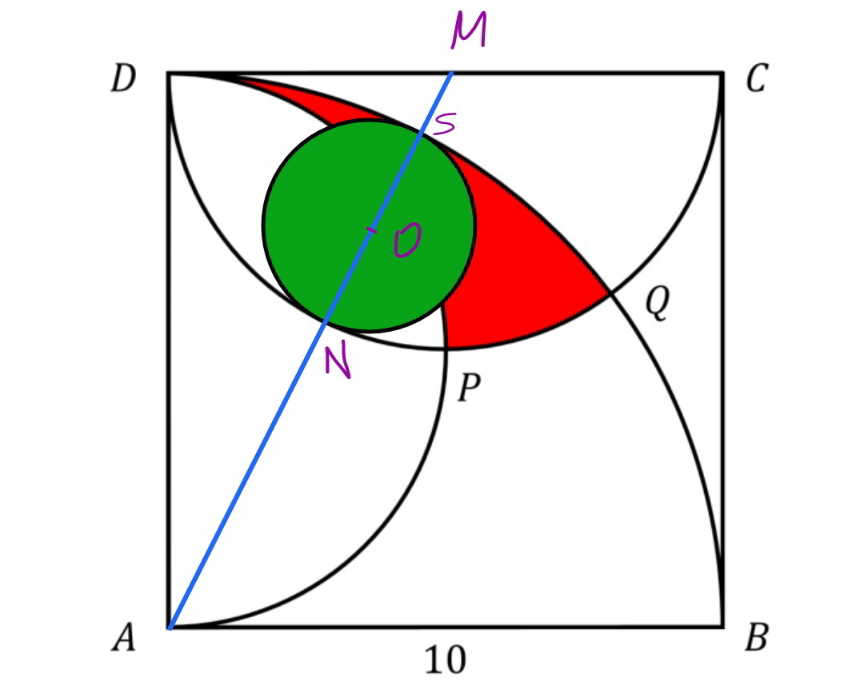
$${AM}=\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }=\mathrm{5}\sqrt{\mathrm{5}} \\ $$$${r}={radius}\:{of}\:{green}\:{circle} \\ $$$${SM}=\mathrm{5}−\mathrm{2}{r} \\ $$$${AN}=\mathrm{10}−\mathrm{2}{r} \\ $$$${AM}=\mathrm{10}−\mathrm{2}{r}+\mathrm{2}{r}+\mathrm{5}−\mathrm{2}{r} \\ $$$$\mathrm{5}\sqrt{\mathrm{5}}=\mathrm{15}−\mathrm{2}{r} \\ $$$$\Rightarrow{r}=\frac{\mathrm{5}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)}{\mathrm{2}} \\ $$$${A}_{{green}} =\pi{r}^{\mathrm{2}} =\frac{\mathrm{25}\left(\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}\right)\pi}{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
