Menu Close

Question-173352

Tinku Tara 0 Comments
Pin




Question Number 173352 by cortano1 last updated on 10/Jul/22
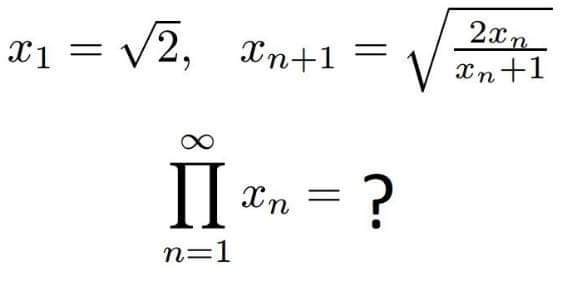
Answered by mr W last updated on 10/Jul/22
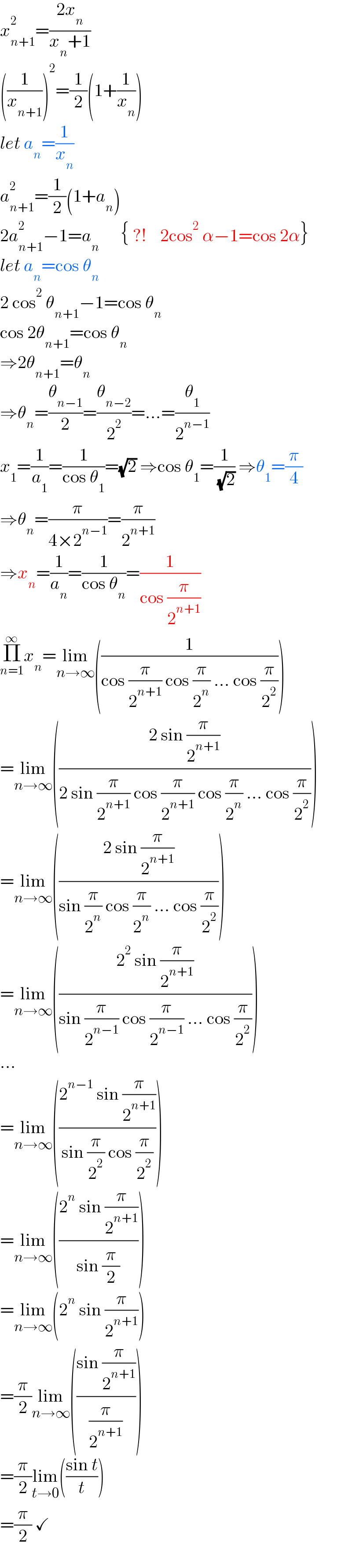
x_(n+1) ^2 =((2x_n )/(x_n +1)) ((1/x_(n+1) ))^2 =(1/2)(1+(1/x_n )) let a_n =(1/x_n ) a_(n+1) ^2 =(1/2)(1+a_n ) 2a_(n+1) ^2 −1=a_n { ?! 2cos^2 α−1=cos 2α} let a_n =cos θ_n 2 cos^2 θ_(n+1) −1=cos θ_n cos 2θ_(n+1) =cos θ_n ⇒2θ_(n+1) =θ_n ⇒θ_n =(θ_(n−1) /2)=(θ_(n−2) /2^2 )=...=(θ_1 /2^(n−1) ) x_1 =(1/a_1 )=(1/(cos θ_1 ))=(√2) ⇒cos θ_1 =(1/( (√2))) ⇒θ_1 =(π/4) ⇒θ_n =(π/(4×2^(n−1) ))=(π/2^(n+1) ) ⇒x_n =(1/a_n )=(1/(cos θ_n ))=(1/(cos (π/2^(n+1) ))) Π_(n=1) ^∞ x_n =lim_(n→∞) ((1/(cos (π/2^(n+1) ) cos (π/2^n ) ... cos (π/2^2 )))) =lim_(n→∞) (((2 sin (π/2^(n+1) ))/(2 sin (π/2^(n+1) ) cos (π/2^(n+1) ) cos (π/2^n ) ... cos (π/2^2 )))) =lim_(n→∞) (((2 sin (π/2^(n+1) ))/(sin (π/2^n ) cos (π/2^n ) ... cos (π/2^2 )))) =lim_(n→∞) (((2^2 sin (π/2^(n+1) ))/(sin (π/2^(n−1) ) cos (π/2^(n−1) ) ... cos (π/2^2 )))) ... =lim_(n→∞) (((2^(n−1) sin (π/2^(n+1) ))/(sin (π/2^2 ) cos (π/2^2 )))) =lim_(n→∞) (((2^n sin (π/2^(n+1) ))/(sin (π/2)))) =lim_(n→∞) (2^n sin (π/2^(n+1) )) =(π/2)lim_(n→∞) (((sin (π/2^(n+1) ))/(π/2^(n+1) ))) =(π/2)lim_(t→0) (((sin t)/t)) =(π/2) ✓
$${x}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{2}{x}_{{n}} }{{x}_{{n}} +\mathrm{1}} \\ $$$$\left(\frac{\mathrm{1}}{{x}_{{n}+\mathrm{1}} }\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}_{{n}} }\right) \\ $$$${let}\:{a}_{{n}} =\frac{\mathrm{1}}{{x}_{{n}} } \\ $$$${a}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{a}_{{n}} \right) \\ $$$$\mathrm{2}{a}_{{n}+\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}={a}_{{n}} \:\:\:\:\:\:\left\{\:?!\:\:\:\:\mathrm{2cos}^{\mathrm{2}} \:\alpha−\mathrm{1}=\mathrm{cos}\:\mathrm{2}\alpha\right\} \\ $$$${let}\:{a}_{{n}} =\mathrm{cos}\:\theta_{{n}} \\ $$$$\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\theta_{{n}+\mathrm{1}} −\mathrm{1}=\mathrm{cos}\:\theta_{{n}} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta_{{n}+\mathrm{1}} =\mathrm{cos}\:\theta_{{n}} \\ $$$$\Rightarrow\mathrm{2}\theta_{{n}+\mathrm{1}} =\theta_{{n}} \\ $$$$\Rightarrow\theta_{{n}} =\frac{\theta_{{n}−\mathrm{1}} }{\mathrm{2}}=\frac{\theta_{{n}−\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }=…=\frac{\theta_{\mathrm{1}} }{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}}{{a}_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{cos}\:\theta_{\mathrm{1}} }=\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{cos}\:\theta_{\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\theta_{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$$$\Rightarrow\theta_{{n}} =\frac{\pi}{\mathrm{4}×\mathrm{2}^{{n}−\mathrm{1}} }=\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow{x}_{{n}} =\frac{\mathrm{1}}{{a}_{{n}} }=\frac{\mathrm{1}}{\mathrm{cos}\:\theta_{{n}} }=\frac{\mathrm{1}}{\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}{x}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}} }\:…\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}} }\:…\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}} }\:…\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}^{\mathrm{2}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{{n}−\mathrm{1}} }\:…\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }}\right) \\ $$$$… \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}^{{n}−\mathrm{1}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }\:\mathrm{cos}\:\frac{\pi}{\mathrm{2}^{\mathrm{2}} }}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}^{{n}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\mathrm{sin}\:\frac{\pi}{\mathrm{2}}}\right) \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{2}^{{n}} \:\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}{\frac{\pi}{\mathrm{2}^{{n}+\mathrm{1}} }}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{t}}{{t}}\right) \\ $$$$=\frac{\pi}{\mathrm{2}}\:\checkmark \\ $$
Commented by aleks041103 last updated on 10/Jul/22
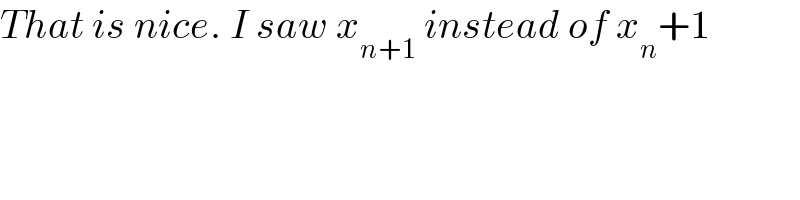
That is nice. I saw x_(n+1) instead of x_n +1
$${That}\:{is}\:{nice}.\:{I}\:{saw}\:{x}_{{n}+\mathrm{1}} \:{instead}\:{of}\:{x}_{{n}} +\mathrm{1} \\ $$
Commented by mr W last updated on 10/Jul/22
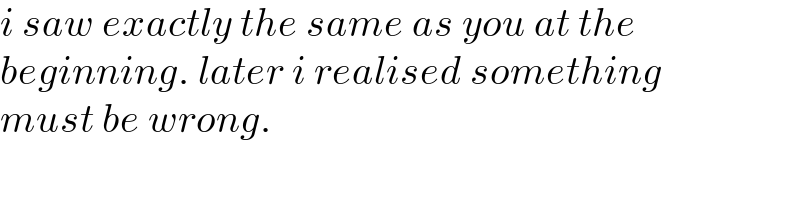
i saw exactly the same as you at the beginning. later i realised something must be wrong.
$${i}\:{saw}\:{exactly}\:{the}\:{same}\:{as}\:{you}\:{at}\:{the} \\ $$$${beginning}.\:{later}\:{i}\:{realised}\:{something} \\ $$$${must}\:{be}\:{wrong}. \\ $$
Commented by Tawa11 last updated on 11/Jul/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *