Question Number 173386 by mathlove last updated on 10/Jul/22

Answered by mnjuly1970 last updated on 10/Jul/22
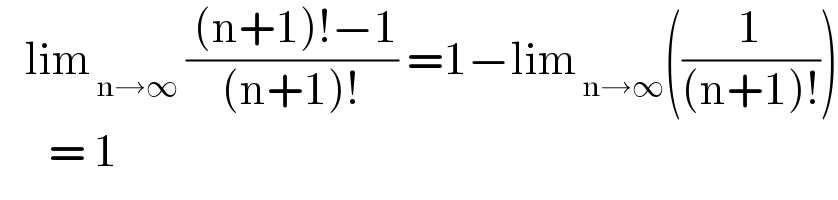
$$\:\:\:\mathrm{lim}_{\:\mathrm{n}\rightarrow\infty} \:\frac{\:\left(\mathrm{n}+\mathrm{1}\right)!−\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}\:=\mathrm{1}−\mathrm{lim}_{\:\mathrm{n}\rightarrow\infty} \left(\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}\right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{1} \\ $$
Commented by mr W last updated on 11/Jul/22

$${that}\:{you}\:{don}'{t}\:{understand}\:{it}\:{doesn}'{t} \\ $$$${mean}\:{that}\:{it}\:{is}\:{wrong}! \\ $$$$\mathrm{1}×\mathrm{1}!=\left(\mathrm{2}−\mathrm{1}\right)×\mathrm{1}!=\mathrm{2}!−\mathrm{1}! \\ $$$$\mathrm{2}×\mathrm{2}!=\mathrm{3}!−\mathrm{2}! \\ $$$$\mathrm{3}×\mathrm{3}!=\mathrm{4}!−\mathrm{3}! \\ $$$$… \\ $$$${n}×{n}!=\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$\Sigma=\left({n}+\mathrm{1}\right)!−\mathrm{1}! \\ $$$$\frac{\Sigma}{\left({n}+\mathrm{1}\right)!}=\frac{\left({n}+\mathrm{1}\right)!−\mathrm{1}}{\left({n}+\mathrm{1}\right)!}=\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\Sigma}{\left({n}+\mathrm{1}\right)!}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}\right)=\mathrm{1}−\mathrm{0}=\mathrm{1} \\ $$$${so}\:{it}\:{is}\:{very}\:{correct}! \\ $$
Commented by mathlove last updated on 11/Jul/22

$${thanks}\:{mr}\:{W} \\ $$
Commented by mnjuly1970 last updated on 11/Jul/22
$$\:\:\:\:\mathrm{thx}\:\mathrm{so}\:\mathrm{much}\:\:\mathrm{Sir}\:\:\mathrm{W}… \\ $$
