Question Number 173408 by mr W last updated on 11/Jul/22
Commented by mr W last updated on 11/Jul/22

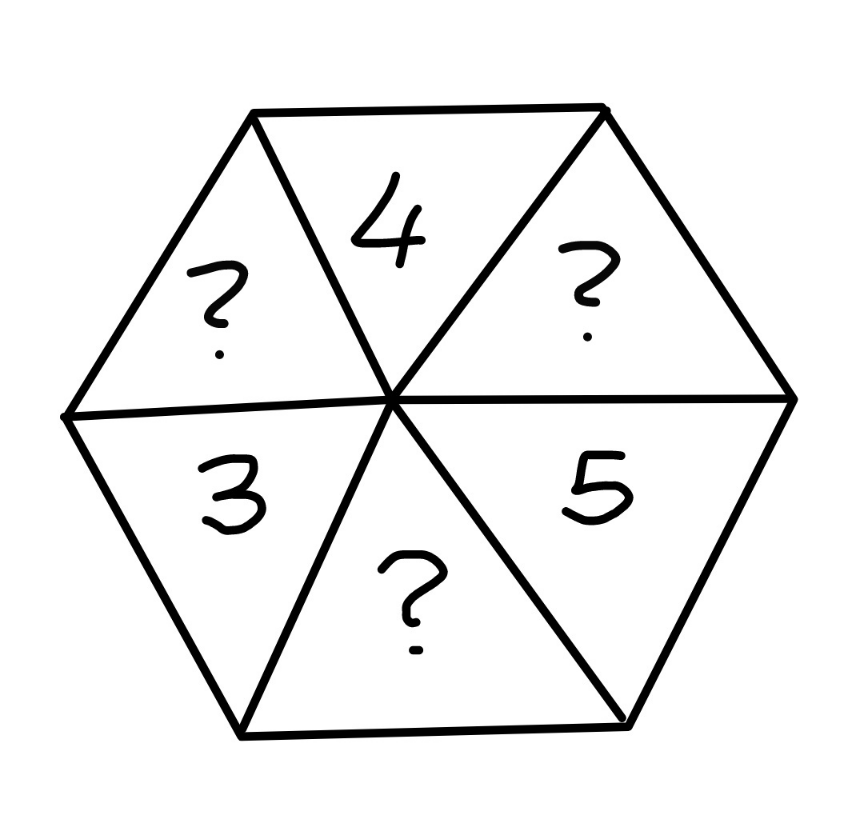
$${the}\:{areas}\:{of}\:{three}\:{parts}\:{of}\:{a}\:{regular} \\ $$$${hexagon}\:{are}\:{given}.\:{find}\:{the}\:{areas}\:{of} \\ $$$${the}\:{other}\:{parts}. \\ $$
Answered by aleks041103 last updated on 11/Jul/22

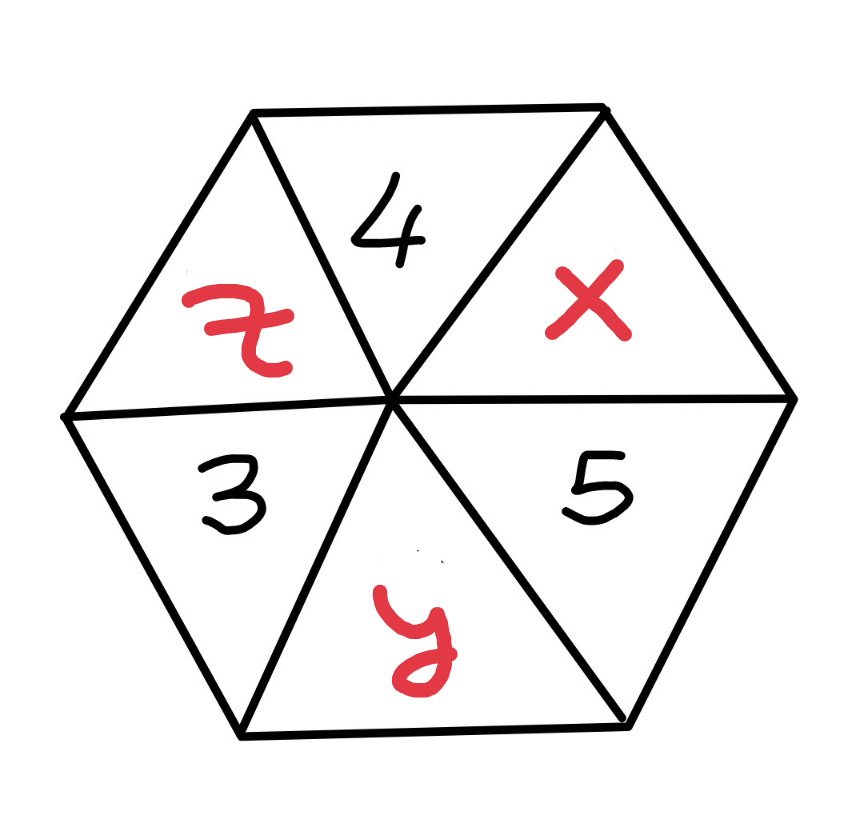
$${if}\:{we}\:{extend}\:{the}\:{sides}\:{we}\:{can}\:{form}\:\mathrm{2} \\ $$$${equlateral}\:{triangles}.\:{In}\:{those},\:{the}\:{sum} \\ $$$${of}\:{the}\:{distances}\:{from}\:{any}\:{point}\:{inside} \\ $$$${to}\:{the}\:{sides}\:{is}\:{constant}\:{independent}\:{of} \\ $$$${the}\:{chosen}\:{point}. \\ $$$$\Rightarrow{S}_{{hex}} =\mathrm{2}\left(\mathrm{3}+\mathrm{4}+\mathrm{5}\right)=\mathrm{2}.\mathrm{12}=\mathrm{24} \\ $$$${The}\:{sum}\:{of}\:{the}\:{distances}\:{from}\:{a}\:{point} \\ $$$${to}\:{two}\:{opposite}\:{sides}\:{is}\:{constant}. \\ $$$$\Rightarrow\mathrm{3}+{x}=\mathrm{4}+{y}=\mathrm{5}+{z}={S}/\mathrm{3}=\mathrm{8} \\ $$$$\Rightarrow{x}=\mathrm{5},{y}=\mathrm{4},{z}=\mathrm{3} \\ $$
Commented by aleks041103 last updated on 11/Jul/22
Commented by mr W last updated on 11/Jul/22

$${great}!\:{thanks}\:{sir}! \\ $$
