Question Number 173420 by AgniMath last updated on 11/Jul/22

Answered by Rasheed.Sindhi last updated on 11/Jul/22
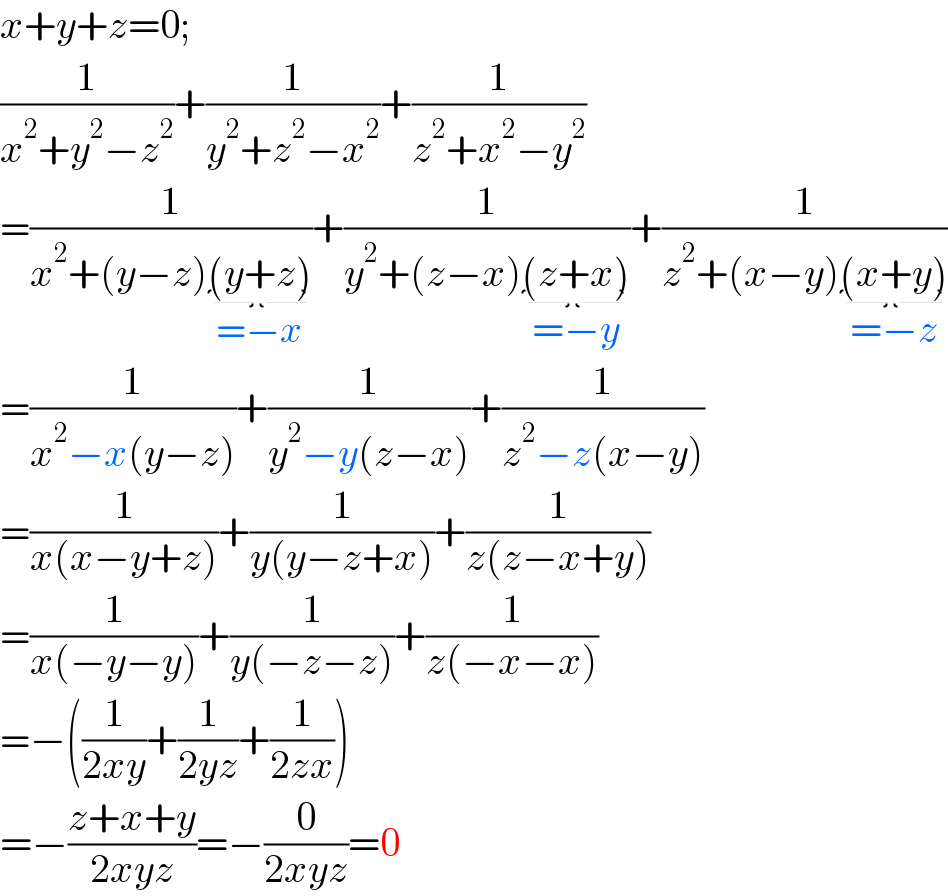
$${x}+{y}+{z}=\mathrm{0}; \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} −{z}^{\mathrm{2}} }+\frac{\mathrm{1}}{{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{z}^{\mathrm{2}} +{x}^{\mathrm{2}} −{y}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\left({y}−{z}\right)\underset{=−{x}} {\underbrace{\left({y}+{z}\right)}}}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} +\left({z}−{x}\right)\underset{=−{y}} {\underbrace{\left({z}+{x}\right)}}}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} +\left({x}−{y}\right)\underset{=−{z}} {\underbrace{\left({x}+{y}\right)}}} \\ $$$$=\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}\left({y}−{z}\right)}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} −{y}\left({z}−{x}\right)}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} −{z}\left({x}−{y}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}\left({x}−{y}+{z}\right)}+\frac{\mathrm{1}}{{y}\left({y}−{z}+{x}\right)}+\frac{\mathrm{1}}{{z}\left({z}−{x}+{y}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}\left(−{y}−{y}\right)}+\frac{\mathrm{1}}{{y}\left(−{z}−{z}\right)}+\frac{\mathrm{1}}{{z}\left(−{x}−{x}\right)} \\ $$$$=−\left(\frac{\mathrm{1}}{\mathrm{2}{xy}}+\frac{\mathrm{1}}{\mathrm{2}{yz}}+\frac{\mathrm{1}}{\mathrm{2}{zx}}\right) \\ $$$$=−\frac{{z}+{x}+{y}}{\mathrm{2}{xyz}}=−\frac{\mathrm{0}}{\mathrm{2}{xyz}}=\mathrm{0} \\ $$
