Question-173445

Question Number 173445 by AgniMath last updated on 11/Jul/22

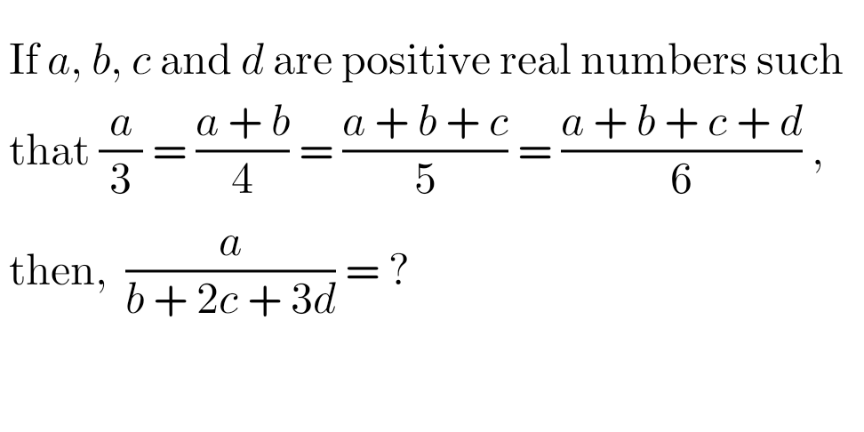
Answered by Rasheed.Sindhi last updated on 11/Jul/22

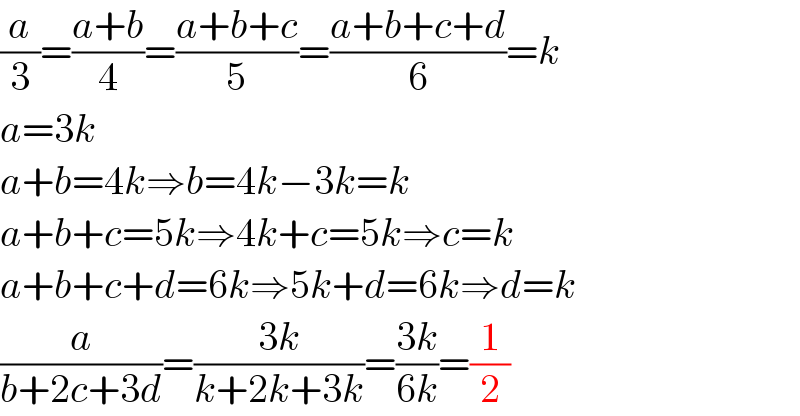
(a/3)=((a+b)/4)=((a+b+c)/5)=((a+b+c+d)/6)=k a=3k a+b=4k⇒b=4k−3k=k a+b+c=5k⇒4k+c=5k⇒c=k a+b+c+d=6k⇒5k+d=6k⇒d=k (a/(b+2c+3d))=((3k)/(k+2k+3k))=((3k)/(6k))=(1/2)

$$\frac{{a}}{\mathrm{3}}=\frac{{a}+{b}}{\mathrm{4}}=\frac{{a}+{b}+{c}}{\mathrm{5}}=\frac{{a}+{b}+{c}+{d}}{\mathrm{6}}={k} \\ $$$${a}=\mathrm{3}{k} \\ $$$${a}+{b}=\mathrm{4}{k}\Rightarrow{b}=\mathrm{4}{k}−\mathrm{3}{k}={k} \\ $$$${a}+{b}+{c}=\mathrm{5}{k}\Rightarrow\mathrm{4}{k}+{c}=\mathrm{5}{k}\Rightarrow{c}={k} \\ $$$${a}+{b}+{c}+{d}=\mathrm{6}{k}\Rightarrow\mathrm{5}{k}+{d}=\mathrm{6}{k}\Rightarrow{d}={k} \\ $$$$\frac{{a}}{{b}+\mathrm{2}{c}+\mathrm{3}{d}}=\frac{\mathrm{3}{k}}{{k}+\mathrm{2}{k}+\mathrm{3}{k}}=\frac{\mathrm{3}{k}}{\mathrm{6}{k}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by mahdipoor last updated on 11/Jul/22

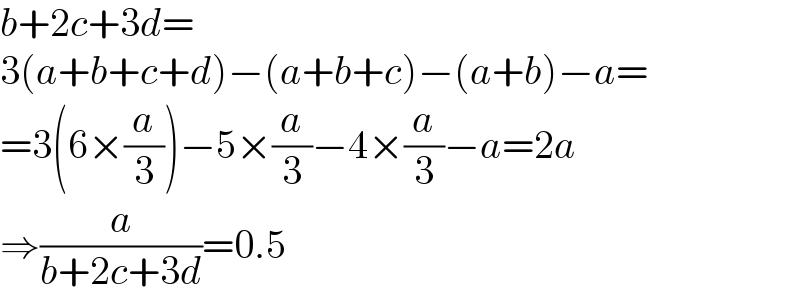
b+2c+3d= 3(a+b+c+d)−(a+b+c)−(a+b)−a= =3(6×(a/3))−5×(a/3)−4×(a/3)−a=2a ⇒(a/(b+2c+3d))=0.5

$${b}+\mathrm{2}{c}+\mathrm{3}{d}= \\ $$$$\mathrm{3}\left({a}+{b}+{c}+{d}\right)−\left({a}+{b}+{c}\right)−\left({a}+{b}\right)−{a}= \\ $$$$=\mathrm{3}\left(\mathrm{6}×\frac{{a}}{\mathrm{3}}\right)−\mathrm{5}×\frac{{a}}{\mathrm{3}}−\mathrm{4}×\frac{{a}}{\mathrm{3}}−{a}=\mathrm{2}{a} \\ $$$$\Rightarrow\frac{{a}}{{b}+\mathrm{2}{c}+\mathrm{3}{d}}=\mathrm{0}.\mathrm{5} \\ $$

Answered by AgniMath last updated on 12/Jul/22

Another way (a/3) = ((a + b)/4) = ((a + b + c)/5) = ((a + b + c + d)/6) (a/3) = ((a + b)/4) or a = 3b (a/3) = ((a + b + c)/5) or a = 3c (a/3) = ((a + b + c + d)/6) or a = 3d (a/(b + 2c + 3d)) = (a/((a/3) + ((2a)/3) + a)) = (a/(2a)) = (1/2)

$$\mathrm{Another}\:\mathrm{way} \\ $$$$\frac{{a}}{\mathrm{3}}\:=\:\frac{{a}\:+\:{b}}{\mathrm{4}}\:=\:\frac{{a}\:+\:{b}\:+\:{c}}{\mathrm{5}}\:=\:\frac{{a}\:+\:{b}\:+\:{c}\:+\:{d}}{\mathrm{6}} \\ $$$$\frac{{a}}{\mathrm{3}}\:=\:\frac{{a}\:+\:{b}}{\mathrm{4}} \\ $$$${or}\:{a}\:=\:\mathrm{3}{b} \\ $$$$\frac{{a}}{\mathrm{3}}\:=\:\frac{{a}\:+\:{b}\:+\:{c}}{\mathrm{5}} \\ $$$${or}\:{a}\:=\:\mathrm{3}{c} \\ $$$$\frac{{a}}{\mathrm{3}}\:=\:\frac{{a}\:+\:{b}\:+\:{c}\:+\:{d}}{\mathrm{6}} \\ $$$${or}\:{a}\:=\:\mathrm{3}{d} \\ $$$$ \\ $$$$\frac{{a}}{{b}\:+\:\mathrm{2}{c}\:+\:\mathrm{3}{d}}\:=\:\frac{{a}}{\frac{{a}}{\mathrm{3}}\:+\:\frac{\mathrm{2}{a}}{\mathrm{3}}\:+\:{a}}\:=\:\frac{{a}}{\mathrm{2}{a}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by bagjagugum123 last updated on 12/Jul/22

$${add}\:{a},{b},{c},{d}\:\neq\mathrm{0} \\ $$

Commented by AgniMath last updated on 12/Jul/22

that's normal

Facebook Tweet Pin

Leave a Reply Cancel reply