Question-173489

Question Number 173489 by AgniMath last updated on 12/Jul/22

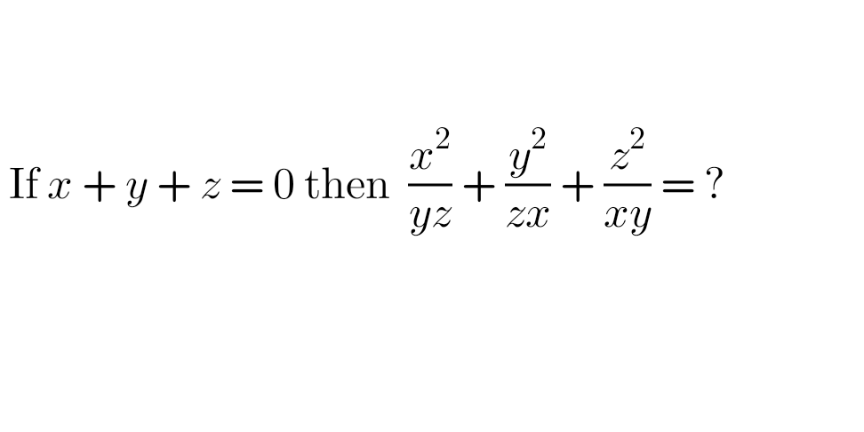
Answered by Rasheed.Sindhi last updated on 12/Jul/22

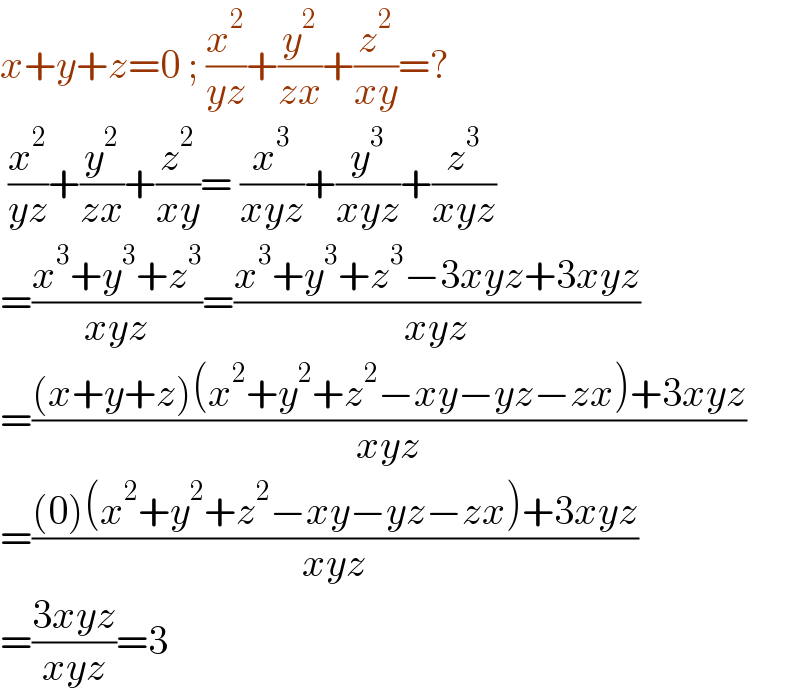
x+y+z=0 ; (x^2 /(yz))+(y^2 /(zx))+(z^2 /(xy))=? (x^2 /(yz))+(y^2 /(zx))+(z^2 /(xy))= (x^3 /(xyz))+(y^3 /(xyz))+(z^3 /(xyz)) =((x^3 +y^3 +z^3 )/(xyz))=((x^3 +y^3 +z^3 −3xyz+3xyz)/(xyz)) =(((x+y+z)(x^2 +y^2 +z^2 −xy−yz−zx)+3xyz)/(xyz)) =(((0)(x^2 +y^2 +z^2 −xy−yz−zx)+3xyz)/(xyz)) =((3xyz)/(xyz))=3

$${x}+{y}+{z}=\mathrm{0}\:;\:\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{zx}}+\frac{{z}^{\mathrm{2}} }{{xy}}=? \\ $$$$\:\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{zx}}+\frac{{z}^{\mathrm{2}} }{{xy}}=\:\frac{{x}^{\mathrm{3}} }{{xyz}}+\frac{{y}^{\mathrm{3}} }{{xyz}}+\frac{{z}^{\mathrm{3}} }{{xyz}} \\ $$$$=\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} }{{xyz}}=\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}+\mathrm{3}{xyz}}{{xyz}} \\ $$$$=\frac{\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)+\mathrm{3}{xyz}}{{xyz}} \\ $$$$=\frac{\left(\mathrm{0}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)+\mathrm{3}{xyz}}{{xyz}} \\ $$$$=\frac{\mathrm{3}{xyz}}{{xyz}}=\mathrm{3} \\ $$

Answered by Rasheed.Sindhi last updated on 12/Jul/22

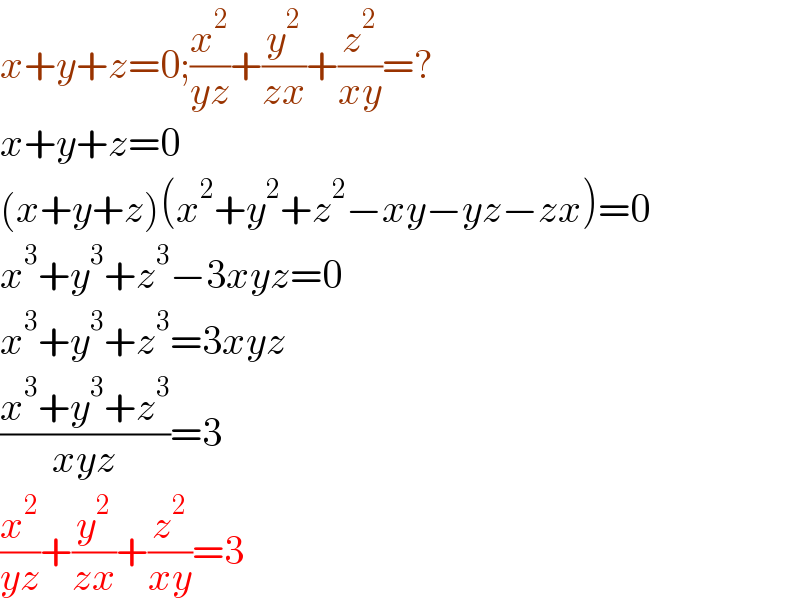
x+y+z=0;(x^2 /(yz))+(y^2 /(zx))+(z^2 /(xy))=? x+y+z=0 (x+y+z)(x^2 +y^2 +z^2 −xy−yz−zx)=0 x^3 +y^3 +z^3 −3xyz=0 x^3 +y^3 +z^3 =3xyz ((x^3 +y^3 +z^3 )/(xyz))=3 (x^2 /(yz))+(y^2 /(zx))+(z^2 /(xy))=3

$${x}+{y}+{z}=\mathrm{0};\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{zx}}+\frac{{z}^{\mathrm{2}} }{{xy}}=? \\ $$$${x}+{y}+{z}=\mathrm{0} \\ $$$$\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} =\mathrm{3}{xyz} \\ $$$$\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} }{{xyz}}=\mathrm{3} \\ $$$$\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{zx}}+\frac{{z}^{\mathrm{2}} }{{xy}}=\mathrm{3} \\ $$

Answered by aleks041103 last updated on 12/Jul/22

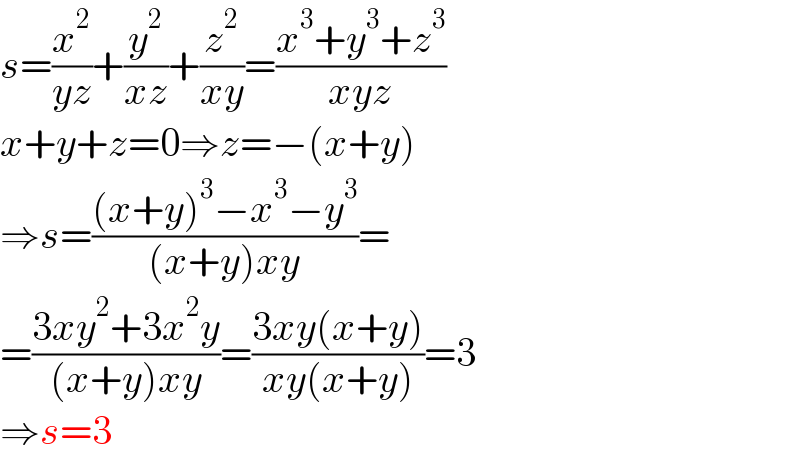
s=(x^2 /(yz))+(y^2 /(xz))+(z^2 /(xy))=((x^3 +y^3 +z^3 )/(xyz)) x+y+z=0⇒z=−(x+y) ⇒s=(((x+y)^3 −x^3 −y^3 )/((x+y)xy))= =((3xy^2 +3x^2 y)/((x+y)xy))=((3xy(x+y))/(xy(x+y)))=3 ⇒s=3

$${s}=\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{xz}}+\frac{{z}^{\mathrm{2}} }{{xy}}=\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} }{{xyz}} \\ $$$${x}+{y}+{z}=\mathrm{0}\Rightarrow{z}=−\left({x}+{y}\right) \\ $$$$\Rightarrow{s}=\frac{\left({x}+{y}\right)^{\mathrm{3}} −{x}^{\mathrm{3}} −{y}^{\mathrm{3}} }{\left({x}+{y}\right){xy}}= \\ $$$$=\frac{\mathrm{3}{xy}^{\mathrm{2}} +\mathrm{3}{x}^{\mathrm{2}} {y}}{\left({x}+{y}\right){xy}}=\frac{\mathrm{3}{xy}\left({x}+{y}\right)}{{xy}\left({x}+{y}\right)}=\mathrm{3} \\ $$$$\Rightarrow{s}=\mathrm{3} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply