Question Number 173610 by AgniMath last updated on 14/Jul/22
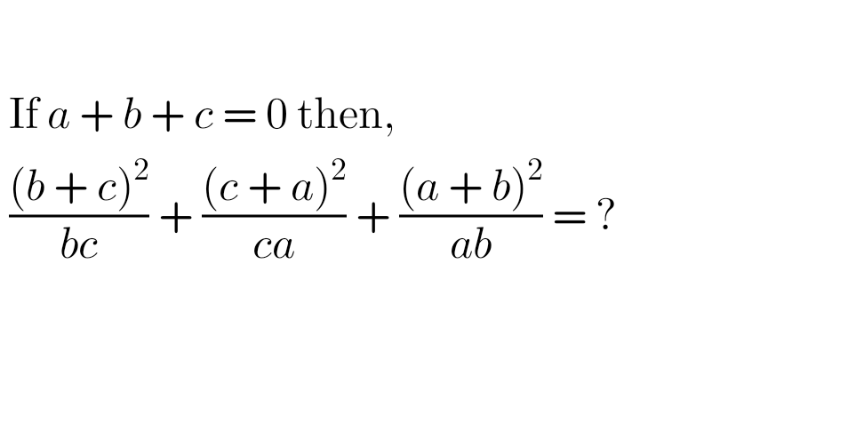
Answered by okbruh123 last updated on 14/Jul/22

$$\boldsymbol{\mathrm{M}{ethod}}\:\mathrm{1}\:: \\ $$$${as}\:{far}\:{as}\:{i}\:{know},\:{this}\:{is}\:{problem}\:{of}\:{prmo}. \\ $$$${its}\:{objective}\:{exam},\:{so}\:{take}\:{any}\:{a},{b},{c}\:{following}\:\Sigma{a}=\mathrm{0} \\ $$$${let}'{s}\:{say}\:−\mathrm{3},+\mathrm{1},+\mathrm{2} \\ $$$${youll}\:{get}\:\frac{\mathrm{9}}{\mathrm{2}}+\frac{\mathrm{1}}{−\mathrm{6}}+\frac{\mathrm{4}}{−\mathrm{3}}=\frac{\mathrm{27}−\mathrm{1}−\mathrm{8}}{\mathrm{6}}=\mathrm{3} \\ $$$$\boldsymbol{{Aliter}}\:: \\ $$$${if}\:{u}\:{wanna}\:{do}\:{legit}, \\ $$$$\Rightarrow\frac{\left({b}+{c}\right)^{\mathrm{2}} {a}+\left({a}+{c}\right)^{\mathrm{2}} {b}+\left({a}+{b}\right)^{\mathrm{2}} {c}}{{abc}} \\ $$$$\Rightarrow{a}+{b}+{c}=\mathrm{0}\:\Rightarrow\:{b}+{c}=−{a}\:{and}\:{symmetrically}\:{you}\:{can}\:{solve}\:{for}\:{a}+{c}\:{anda}+{b} \\ $$$$\Rightarrow\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{{abc}}\:\Rightarrow\:\frac{\underset{=\mathrm{0}} {\underbrace{\left({a}+{b}+{c}\right)}}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{ab}−{bc}−{ca}\right)+\mathrm{3}{abc}}{{abc}} \\ $$$$\Rightarrow\frac{\mathrm{3}{abc}}{{abc}}=\mathrm{3} \\ $$
Commented by Tawa11 last updated on 14/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by behi834171 last updated on 14/Jul/22
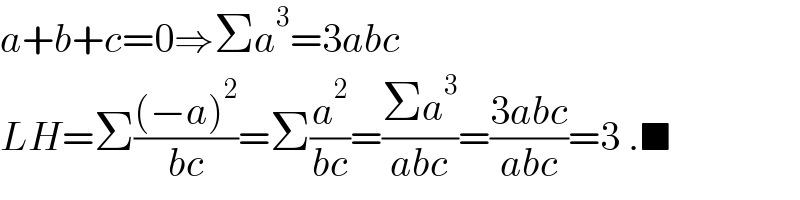
$${a}+{b}+{c}=\mathrm{0}\Rightarrow\Sigma{a}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$$${LH}=\Sigma\frac{\left(−{a}\right)^{\mathrm{2}} }{{bc}}=\Sigma\frac{{a}^{\mathrm{2}} }{{bc}}=\frac{\Sigma{a}^{\mathrm{3}} }{{abc}}=\frac{\mathrm{3}{abc}}{{abc}}=\mathrm{3}\:.\blacksquare \\ $$
